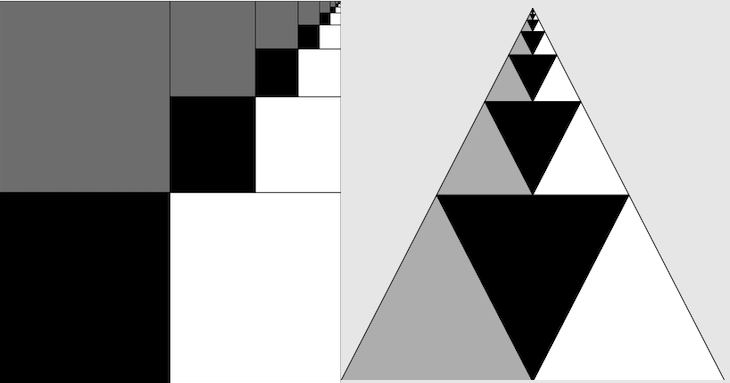
Somme des puissances inverses de quatre

En mathématiques, une série est la somme de plusieurs nombres, dont le nombre peut être fini ou même infini. L’ensemble des nombres dont on fait la somme forme ce que l’on appelle une série. Combien d’éléments contient la séquence?

• S’il s’agit d’une séquence finie, cela signifie que nous avons un nombre limité d’éléments sur lesquels nous faisons la somme, la somme de cette séquence est une suitefinie. Example: La somme des $n$ nombres entiers impairs et Somme de Gauss
• Alternativement, une série infinite est le résultat de l’addition d’une séquence de nombres infinie. L’utilisation de la limite permet de déterminer si une série infinie converge ou diverge. Prenons un exemple!

Prenez votre peinture et vos pinceaux! Nous peignons une toile

Nous commençons par une toile vide et carrée,

et nous voulons peindre $\frac{1}{4}$ en bleu:

Nous obtenons donc quelque chose comme ceci. Maintenant, nous voulons peindre un autre $\frac{1}{16}$ en bleu:

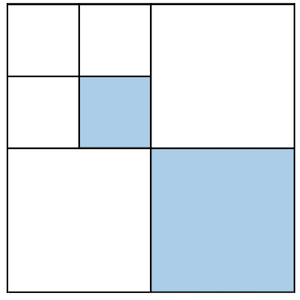
Voici le résultat. Nous avons donc peint en plus $\frac{1}{4}$ de $\frac{1}{4}$ de la toile originale. Nous poursuivons avec $\frac{1}{64}$:

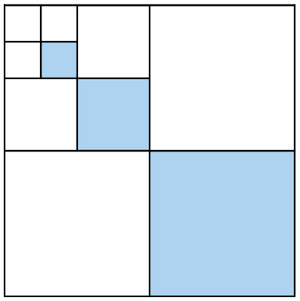
Nous peignons ensuite $\frac{1}{4}\times \frac{1}{64}=\frac{1}{256}$.

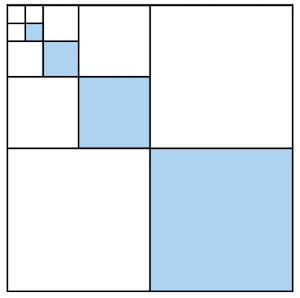
Ensuite, nous peignons en bleu un autre $\frac{1}{1024}$:

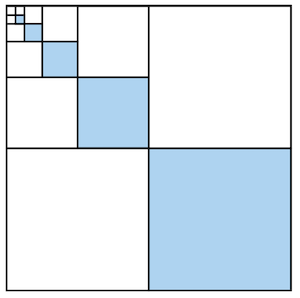
On peut continuer comme ça, à peindre en bleu ${\frac{1}{4}}^n$ de la surface à chaque étape.

Après chaque étape, nous avons trois carrés identiques, dont l’un est entièrement peint en bleu et les deux autres sont laissés en blanc. À la quatrième étape, le motif se répète à une échelle plus petite, nous avons à nouveau un carré bleu et deux carrés blancs. Ce schéma se poursuit à l’infini, de sorte que pour chaque échelle, il y a un carré bleu et deux carrés blancs. Au total, nous avons donc peint $\frac{1}{3}$ la toile en bleu. Le motif bleu représente la somme des puissances inverses de quatre, et nous pouvons donc conclure que la somme des puissances inverses de quatre converge vers $\frac{1}{3}$.

Essayez vous-même

Utilisez le curseur ci-dessous pour voir comment le tableau converge vers le modèle susmentionné pour différentes valeurs de $n$.

Les mathématiques à l’œuvre