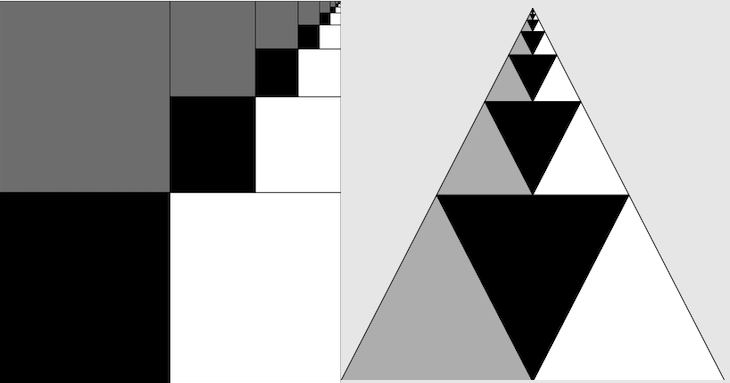
Die Summe negativer Potenzen von 4

In der Mathematik ist eine Reihe definiert als die Summe der Elemente einer zugehörigen Folge, also schlicht eine Summe von Zahlen. Je nachdem wie viele Elemente die Folge besitzt, nennen wir die Reihe

• endlich, wenn die zugehörige Folge endlich ist, das heißt wenn wir nur eine endliche Anzahl an Zahlen zusammenaddieren. Ein Beispiel dafür ist die die Summe der ersten $n$ ungeraden Zahlen und die Gaußsche Summenformel.
• unendlich, wenn die zugehörige Folge kein Ende hat. Durch die Nutzung von Grenzwerten können wir herausfinden, ob die Reihe konvergiert (also sich einem bestimmten endlichen Wert annähert) oder das nicht tut; wir sagen dann, dass die Reihe divergiert. Wir starten mit einem Beispiel!

Holt die Pinsel raus: Wir bemalen eine Leinwand

Wir haben den Auftrag bekommen eine wunderschön leere, quadratische Leinwand zu bemalen.

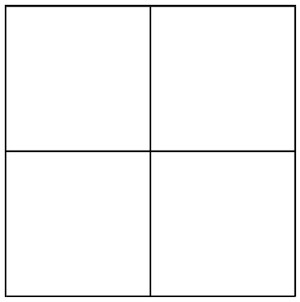
Wir fangen an genau $\frac{1}{4}$ des Quadrats blau anzumalen. Das Ganze sieht dann in etwa so aus.

Als nächstes bemalen wir $\frac{1}{16}$, also $\frac{1}{4}$ von $\frac{1}{4}$, der Fläche blau, was dann so ausschaut.

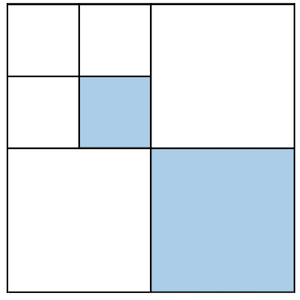
Weiter geht’s mit $\frac{1}{64}$, also $\frac{1}{4}$ von $\frac{1}{16}$.

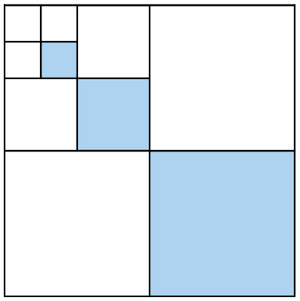
Wir fahren nach diesem Muster fort und bemalen nun $\frac{1}{4}\times \frac{1}{64}=\frac{1}{256}$.

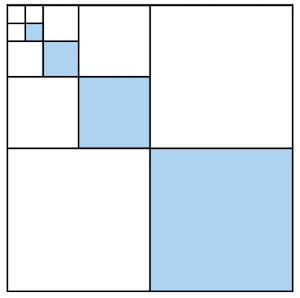
Danach bemalen wir wieder $\frac{1}{4}$ der vorherigen Fläche, dieses Mal also $\frac{1}{1024}$.

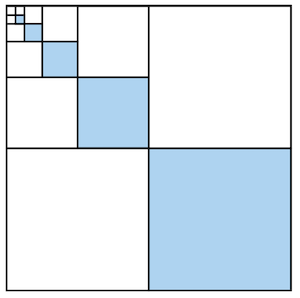
Wir machen immer so weiter und bemalen im $n$-ten Schritt genau ${\frac{1}{4}}^n$ der Fläche blau.

Nach jedem Schritt haben wir genau 3 gleich große Quadrate von dem jeweils eins blau und die anderen beiden weiß sind. Im vierten Quadrat findet sich genau das selbe Muster im kleineren Maßstab, auch hier ist wieder eins der Quadrate blau und die anderen beiden weiß. Dieses Muster wiederholt sich unendlich und demnach haben wir am Ende genau $\frac{1}{3}$ unserer Leinwand blau angemalt. Dieses blaue Muster repräsentiert die inversen Potenzen der Zahl 4 und wir können daraus schließen, dass die Summe der inversen Potenzen von 4 im Grenzwert genau $\frac{1}{3}$ ist.

Versuch’s selbst

Nutze den Schieber um zu sehen, wie sich der Malprozess mit jedem Schritt dem genannten Muster annähert.

Die Mathematik dahinter