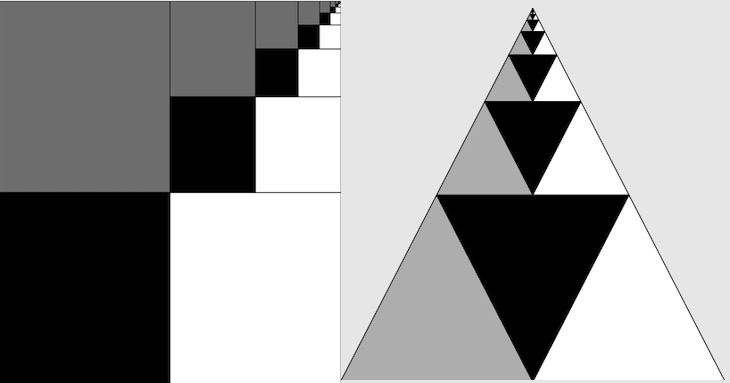
Sum of inverse powers of four

In mathematics, a series is the sum of several numbers, of which there may be finitely or even infinitely many. All the numbers, which we sum over, form a so-called sequence.

How many elements are in the sequence?

• If we are dealing with a finite sequence, meaning we have a limited number of elements we sum over, the sum of that sequence is a finite series. Example: The sum of $n$ odd integers and Gauss Summation
• Alternatively, an infinite series is the result of adding up an infinite sequence of numbers. Through the use of limit we can determine if an infinite series converges or diverges. Let’s look at an example!

Get your paint and brushes! We are painting a canvas

We start with an empty, square Canvas,

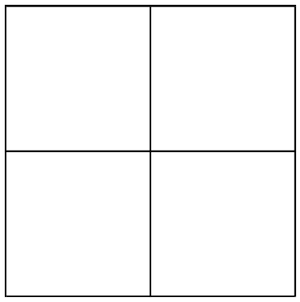
and we want to paint $\frac{1}{4}$ of it blue:

So we end up with something like this. Now, we want to paint another $\frac{1}{16}$ blue:

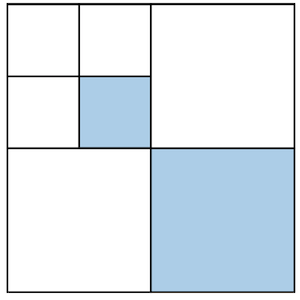
This would be the resulting look. So we additionally painted $\frac{1}{4}$-th of $\frac{1}{4}$-th of the original canvas. We continue with $\frac{1}{64}$:

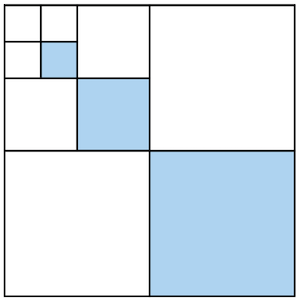
We then paint $\frac{1}{4}\times \frac{1}{64}=\frac{1}{256}$.

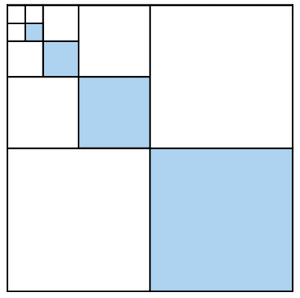
After that we paint blue another $\frac{1}{1024}$:

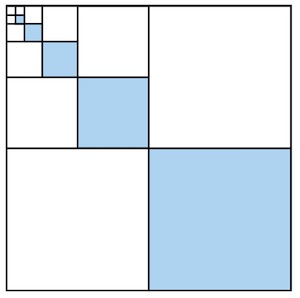
We can go on like this, painting blue ${\frac{1}{4}}^n$ of the surface in every step.

After every step, we have three identical squares, one of which is painted completely blue and the other two are left blank. In the fourth step, the pattern repeats on a smaller scale, we again have one blue and two white squares. This pattern continues infinitely, so that for every scale there is one blue and two white squares. So overall we have painted $\frac{1}{3}$ of the canvas blue. The blue pattern represents the sum of inverse power of four, and so we can conclude that the sum of inverse powers of 4 converges to $\frac{1}{3}$.

Try it yourself

Use the slider below to see how the painting converges to the above-mentioned pattern for different values of $n$.

The math behind it