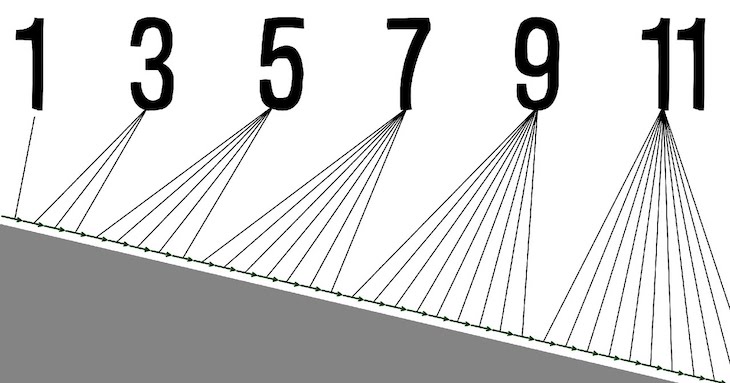
La somme de n entiers impairs

Les nombres impairs sont tous les entiers qui ont un reste de un lorsqu’ils sont divisés par deux. Si $n$ est un nombre entier, la forme générale d’un nombre impair serait $2n-1$, et de tels nombres seraient : 1, 3, 5, 7, 9, 11, 13…

La somme des $n$ entiers impairs n’est rien d’autre que la sommation (l’addition) d’une série de nombres impairs commençant à 1 jusqu’à un certain $n$.

Découvrir des modèles

Commençons par de petits nombres et additionnons-les :

• les 2 premiers nombres impairs. 1 + 3 = 4
• les 3 premiers nombres impairs : 1 + 3 + 5 = 9
• les 4 premiers nombres impairs : 1 + 3 + 5 + 7 = 16

Voyez-vous une tendance se dessiner ?

Si vous ne l’avez pas encore remarqué, ce schéma indique que si nous additionnons les premiers $n$ nombres impairs, le résultat est $n^2$. Il se peut que nous soyons sur la bonne voie, vérifions si ce modèle est valable.

Les sommes des nombres impairs sont-elles liées aux nombres carrés ?

Jusqu’à présent, le modèle semble prometteur, mais nous devons encore nous assurer qu’il ne s’agit pas d’une simple coïncidence.

Réfléchissons aux différentes façons de représenter les nombres carrés. Un candidat trivial et très logique serait un carré de largeur et de hauteur égales.

Prenons par exemple les deux premiers nombres impairs, 1 et 3, et représentons-les par des ensembles de carrés :

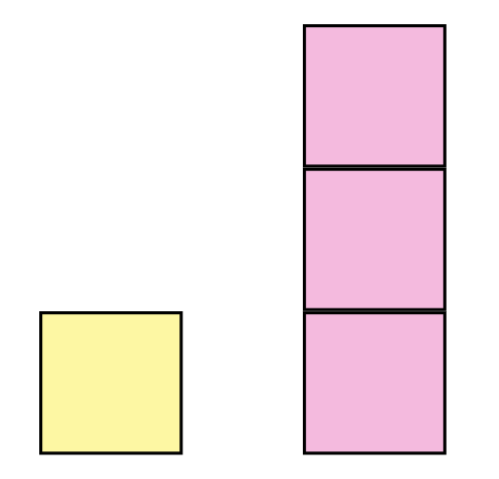
Puisque nous cherchons une représentation visuelle de $2^2$, dans ce cas, la représentation la plus utile de 4 blocs serait la suivante :

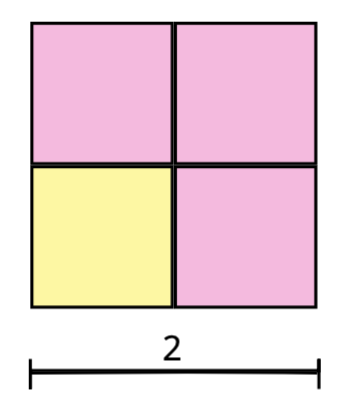
Cette représentation convient parfaitement puisque notre carré de largeur 2 est constitué de 4 briques.

Ajoutons le nombre impair suivant, 5, aux blocs existants.

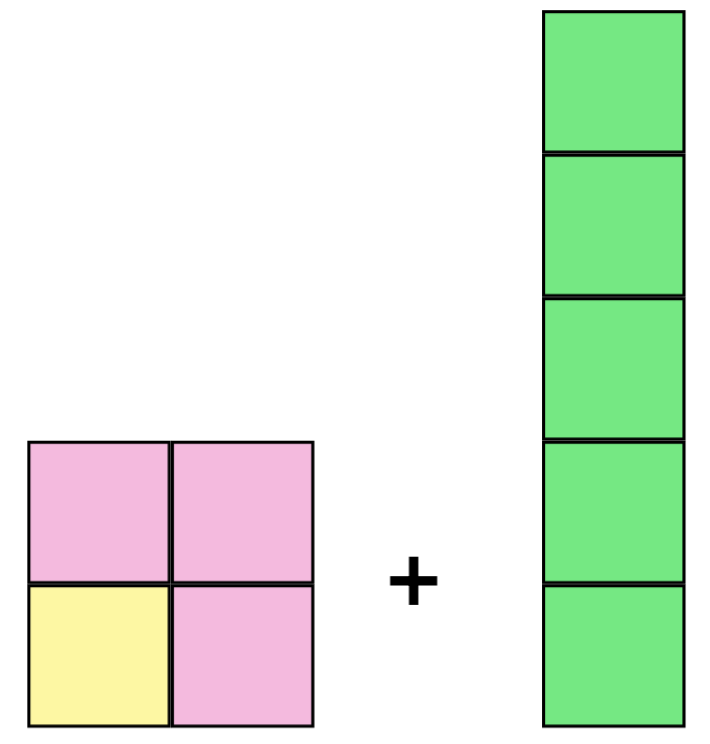
Si nous essayons de l’ajouter gentiment au premier carré, cela ressemblerait à ceci :

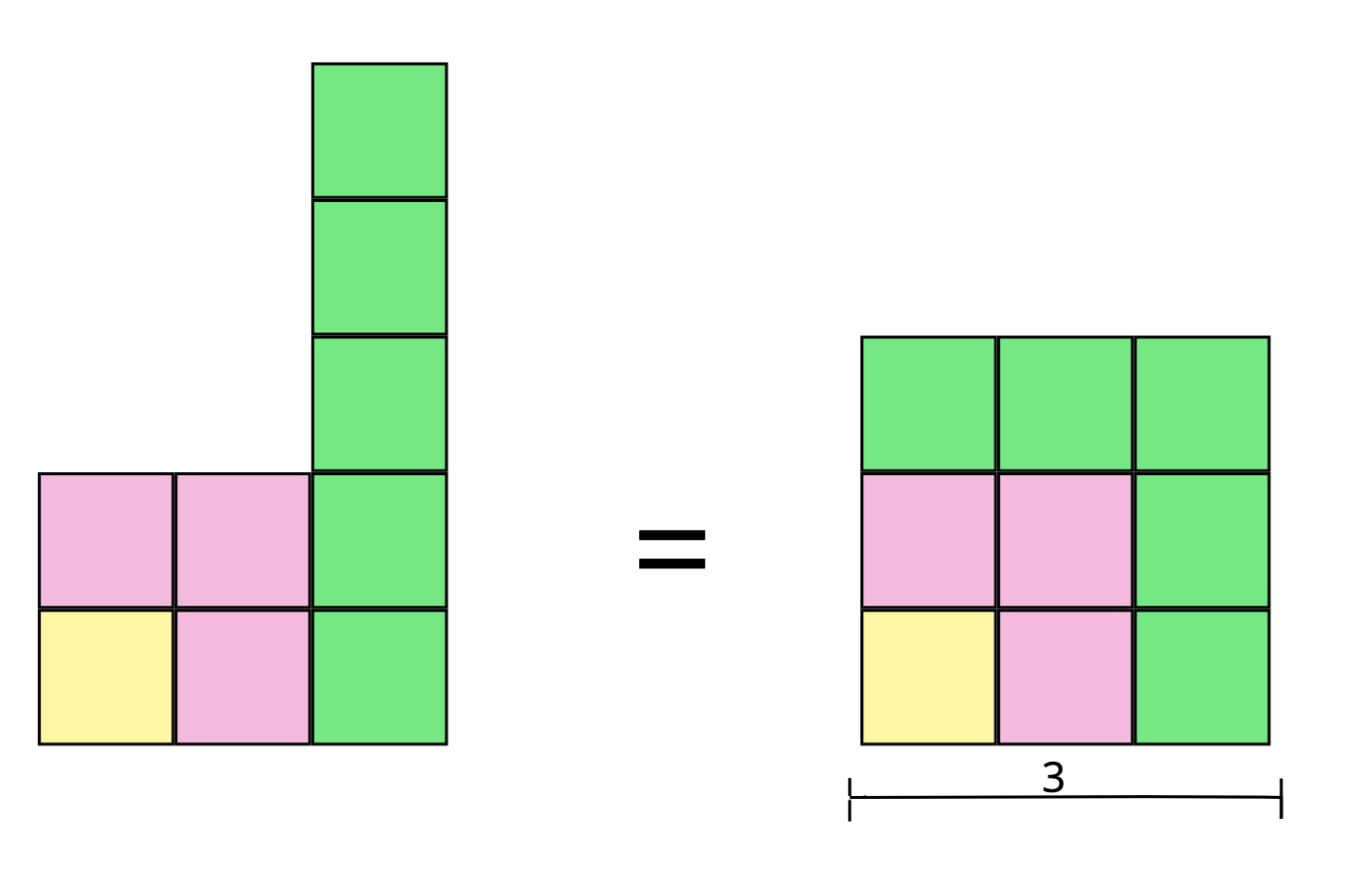
Pour atteindre le nombre impair suivant, il suffit d’ajouter 2 au nombre impair précédent. De même, à chaque étape, nous avons besoin de 2 briques de plus qu’auparavant pour atteindre la case suivante. Bien que nous n’ayons illustré cela que pour $n=3$, nous pouvons voir que ce modèle est valable !

Essayez vous-même

Utilisez le curseur ci-dessous pour le tester pour différentes valeurs de $n$.

Les mathématiques à l’œuvre

La formule pour calculer ce modèle est la suivante