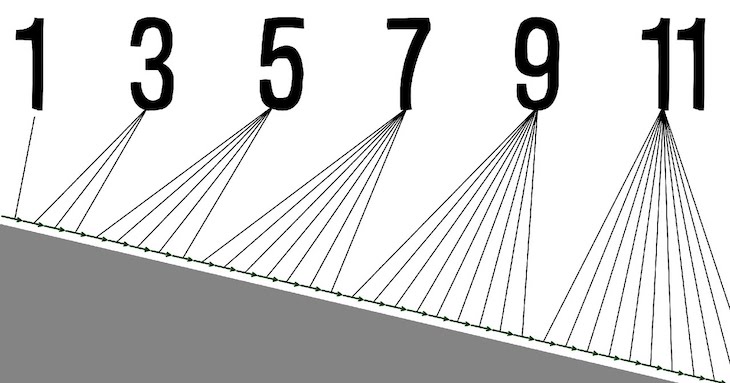
Die Summe von n ungeraden Zahlen

Ungerade Zahlen sind alle ganzen Zahlen, die beim Teilen durch 2 einen Rest lassen. Für eine natürliche Zahl $n$ hat die $n$-te ungerade Zahl die Form $2n-1$. Das gibt uns dann die bekannte Folge 1, 3, 5, 7, 9, 11, …

Nun die Frage: Was ist die Summe der ersten $n$ ungeraden Zahlen?

Muster entdecken

Starten wir mit ein paar kleinen Beispielen

• die Summer der ersten beiden ungeraden Zahlen: 1 + 3 = 4
• die Summe der ersten drei ungeraden Zahlen: 1 + 3 + 5 = 9
• die Summe der ersten vier ungeraden Zahlen: 1 + 3 + 5 + 7 = 16

Siehst du das Muster?

Falls es dir noch nicht aufgefallen ist: Es sieht so aus als wäre die Summe der ersten $n$ ungeraden Zahlen genau $n^2$. Können wir zeigen, dass dieses Muster auch für größere Summen gilt?

Hängt die Summe von ungeraden Zahlen mit den Quadratzahlen zusammen?

Das Muster hält bereits für die ersten drei Beispiele, aber wir müssen noch zeigen, dass es auch allgemein gilt und nicht einfach ein Zufall war.

Überlegen wir mal, wie wir die $n$-te Quadratzahl darstellen können. Natürlich mit einem Quadrat, dessen Breite und Höhe genau $n$ enstpricht.

Nehmen wir also die ersten beiden ungeraden Zahlen, 1 und 3, und fügen sie zu einem Quadrat zusammen:

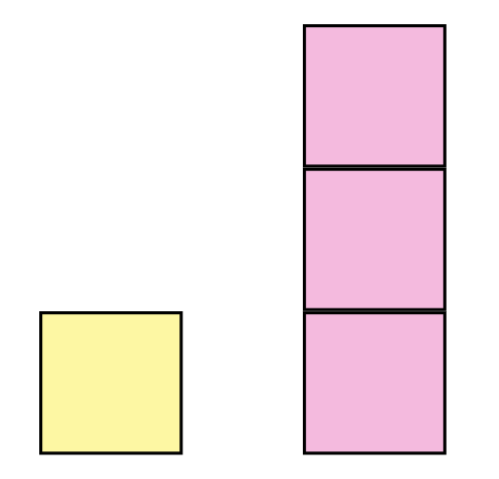
Da wir nach einem Quadrat für die zweite Quadratzahl $2^2$ suchen, können wir die 4 Blöcke wie folgt zusammenfügen:

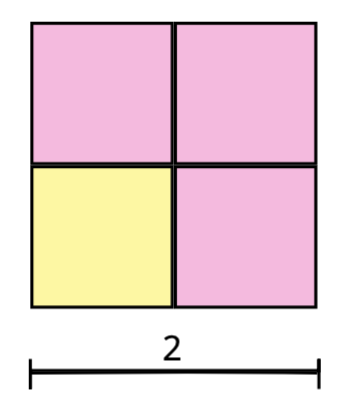
Das passt tatsächlich, schließlich besteht unser Quadrat mit Breite 2 aus genau 4 Blöcken.

Fügen wir nun die nächste ungerade Zahl, 5, zu unseren Blöcken hinzu.

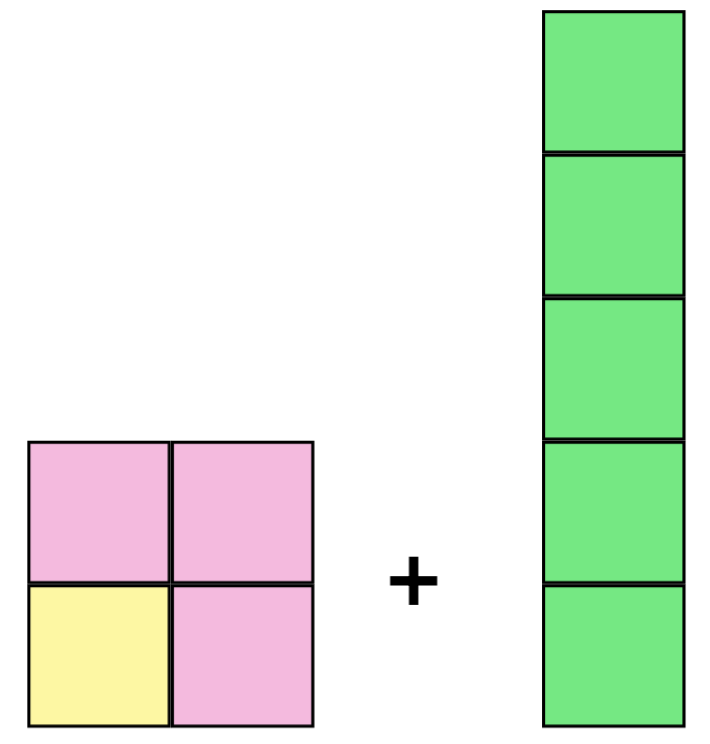
Wenn wir versuchen alles zu einem Quadrat zu ergänzen, sieht es wie folgt aus.

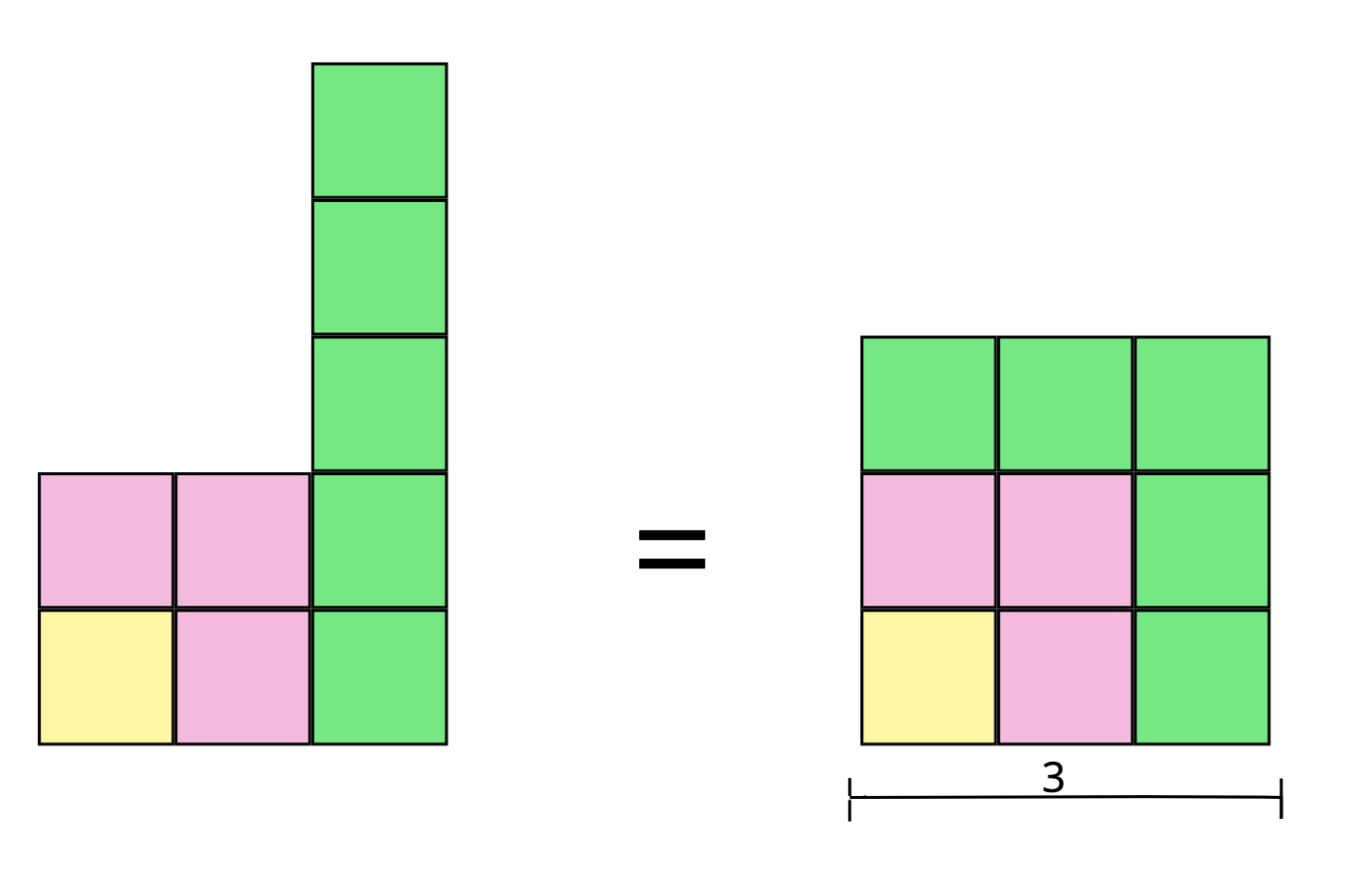
Wenn wir die nächste ungerade Zahl haben wollen, müssen wir 2 zur letzten ungeraden Zahl addieren. Gleichzeitig brauchen wir in jedem Schritt zwei Blöcke mehr, um zum nächst-größeren Quadrat zu gelangen. Obwohl wir diese Idee nur für $n=3$ aufgemalt haben, bleibt dieses Muster auch für größere Zahlen bestehen!

Versuch es selbst

Benutze den Schieber um verschiedene Werte für $n$ auszuprobieren.

Die Mathematik dahinter

Die Formel zu diesem Muster lautet: