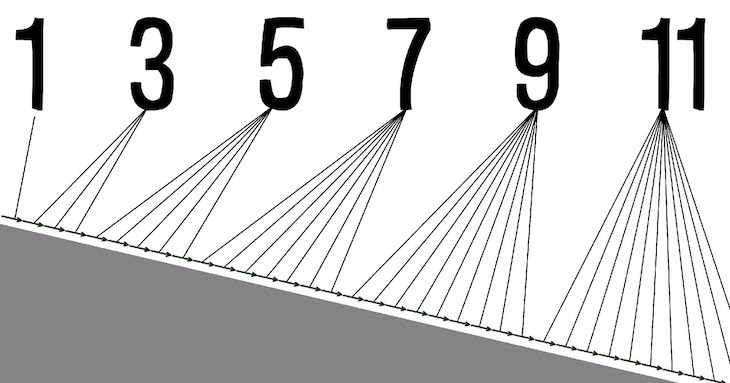
The sum of n odd integers

Odd numbers are all those integers, who have a remainder of one when divided by two. With $n$ being an integer, the general form of an odd number would be $2n-1$, and such numbers would be: 1, 3, 5, 7, 9, 11, 13…

The sum of $n$ odd integers is nothing else but the summation (adding up) of a series of odd numbers starting from 1 up to a certain $n$.

Discovering patterns

Let’s start small and sum up:

• the first 2 odd numbers. 1 + 3 = 4
• the first 3 odd numbers: 1 + 3 + 5 = 9
• the first 4 odd numbers: 1 + 3 + 5 + 7 = 16

Do you see a pattern emerging?

If you haven’t noticed so far, that pattern says that if we add the first $n$ odd numbers then the result is $n^2$. We might be up to something here, let’s check whether this pattern holds.

Are the sums of odd numbers related to square numbers?

Up to this point, the pattern seems to be promising, but we still have to reassure us that this is not just some coincidence.

Let’s think of ways one can represent square numbers. A trivial and very logical candidate would be a square with equal width and height.

Let’s take for instance the first 2 odd numbers 1 and 3, and let’s represent them as sets of squares:

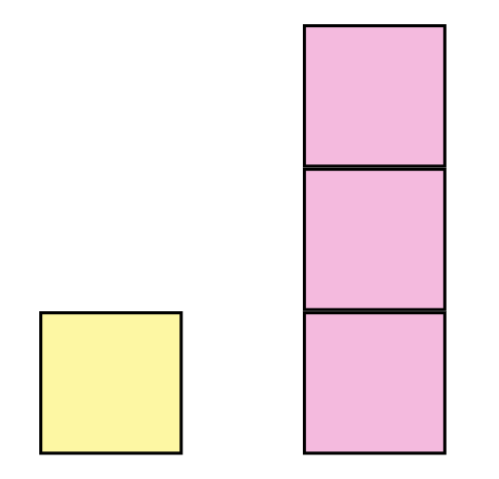
Since we are looking for a visual representation of $2^2$, in this case the most useful representation of 4 blocks would be this:

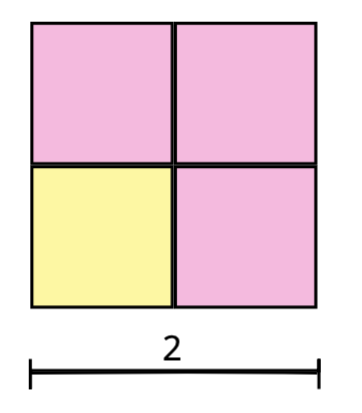
This perfectly fits as our square of width 2 consists of 4 bricks.

Let’s add the next odd number, 5, to the existing blocks.

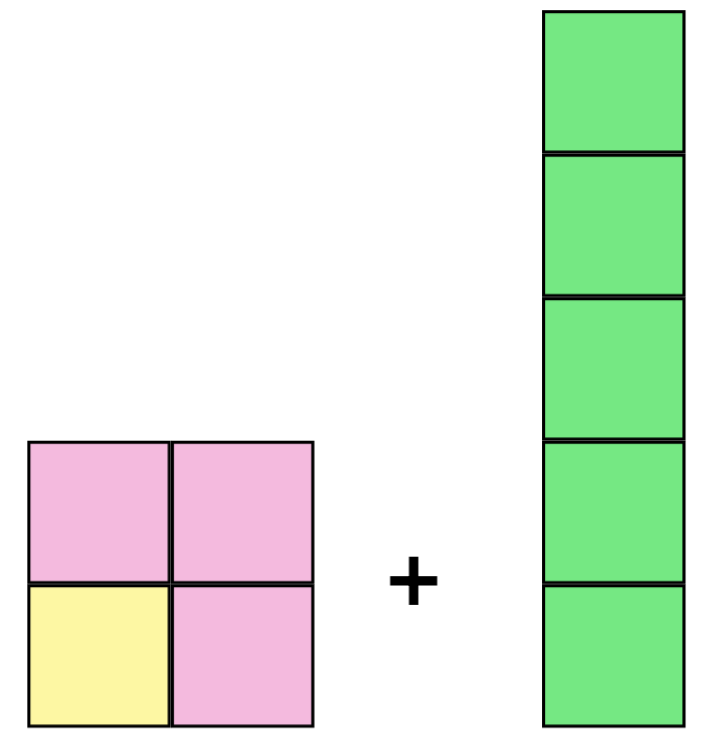
If we try to add it nicely to the first square, it would look something like this:

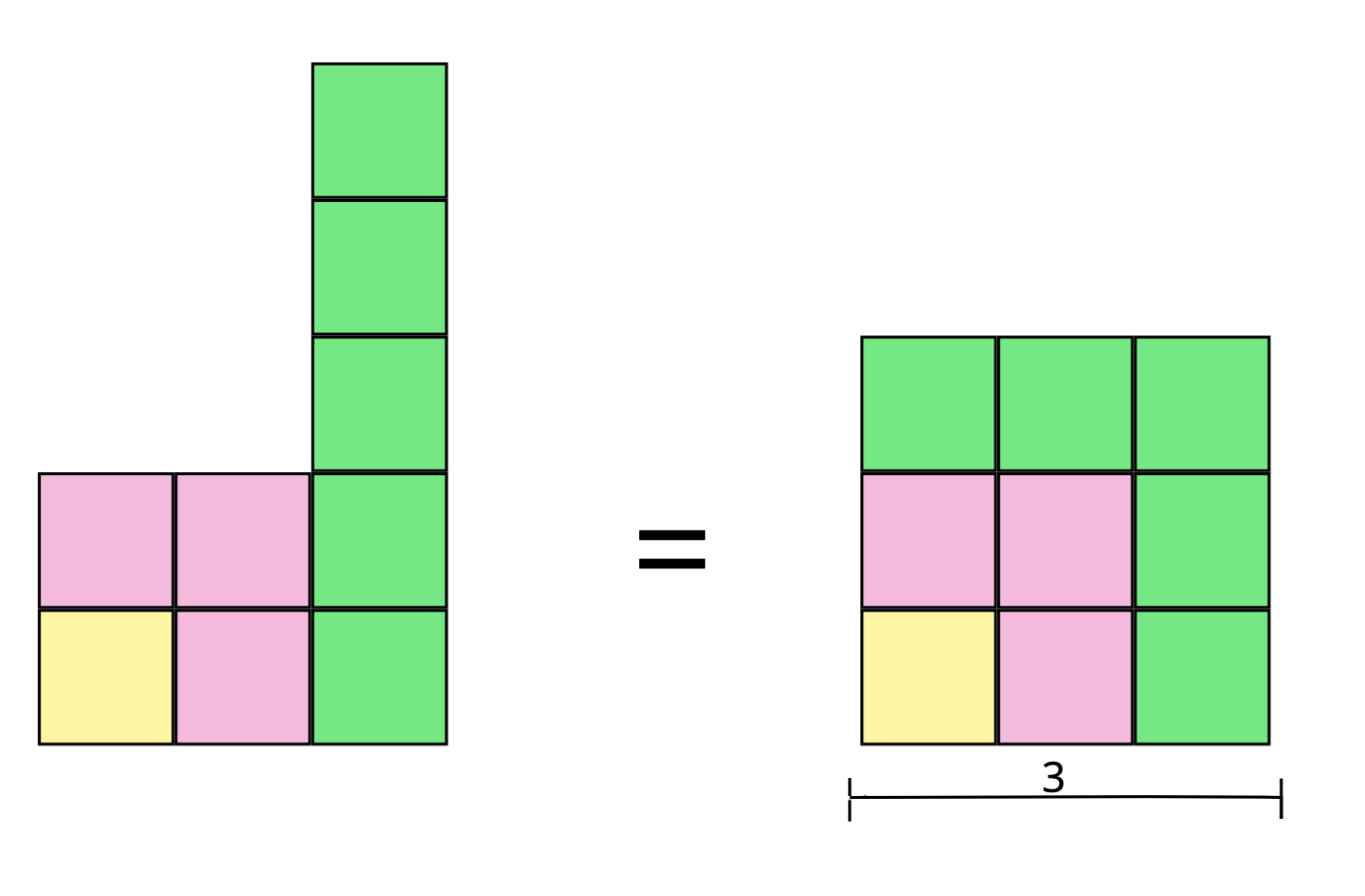
To get to the next odd number we just have to add 2 to the previous odd number. Similarly in every step, we need 2 more bricks than before to get to the next square. Although we only illustrated this for $n=3$, we can see that this pattern holds!

Try it yourself

Use the slider below to test it for different values of $n$.

The math behind it

The formula to calculate this pattern is