Somme de Gauss

Carl Friedrich Gauss (1777-1855 av. J.-C.) est reconnu comme l’un des mathématiciens les plus influents de tous les temps. Il a contribué non seulement Il a contribué non seulement au domaine des mathématiques, mais aussi à celui de la physique et des statistiques. Sa forte intuition numérique a été remarquée dès son plus jeune âge, lorsque son professeur lui a demandé de faire la somme des nombres de un à cent. C’est là qu’il a reconnu un modèle. Il a obtenu cinquante paires de chiffres en additionnant le premier et le dernier chiffre de la série, le deuxième et l’avant-dernier chiffre de la série, et ainsi de suite. Par exemple: (1 + 100), (2 + 99), (3 + 98), …, (50 + 51), et chaque paire a une somme de 101. Donc $50\times 101=5050$.

Comment prouver visuellement la somme des naturels

Imaginons que nous voulions connaître la somme des cinq premiers entiers naturels. Cela signifie que nous devons Au lieu d’écrire les nombres, imaginons que nous sommes des ouvriers du bâtiment et que nous construisons une paire d’escaliers avec des briques de couleur identique. Nous voulons superposer 1 brique, 2 briques, 3 briques, jusqu’à 5 briques. Quelque chose comme ça:

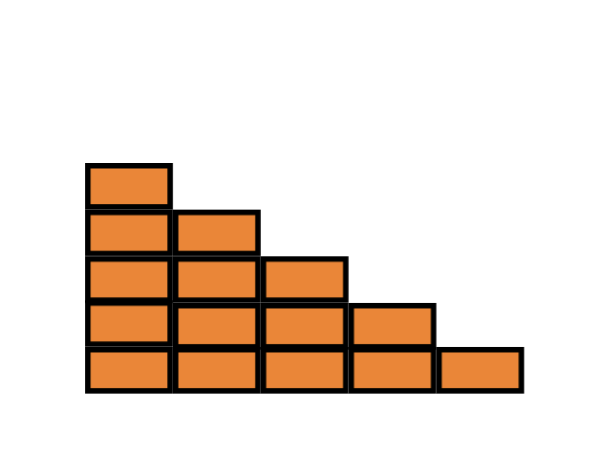
Nous pourrions aller jusqu’à 100 ou 1000 briques, mais 5 briques suffisent pour comprendre l’idée. Comment compter le nombre de briques nécessaires à la construction de l’escalier? Bien sûr, nous pourrions le faire manuellement, mais pourquoi le faire alors qu’il existe un autre moyen plus rapide! Imaginons que nous construisions notre escalier en miroir (en utilisant une autre couleur pour représenter les briques en miroir),

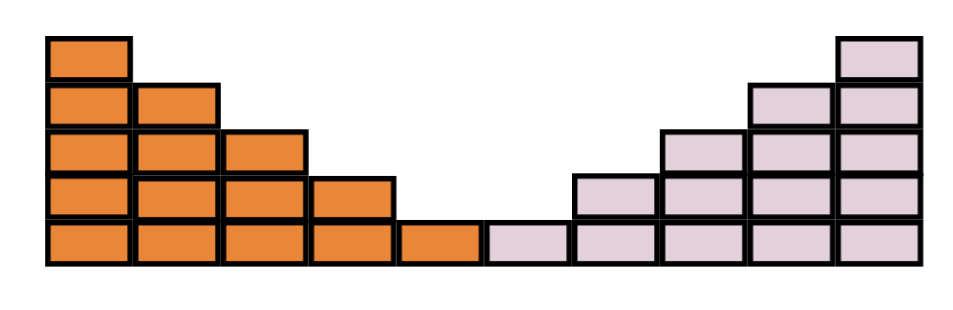
puis nous le renversons:

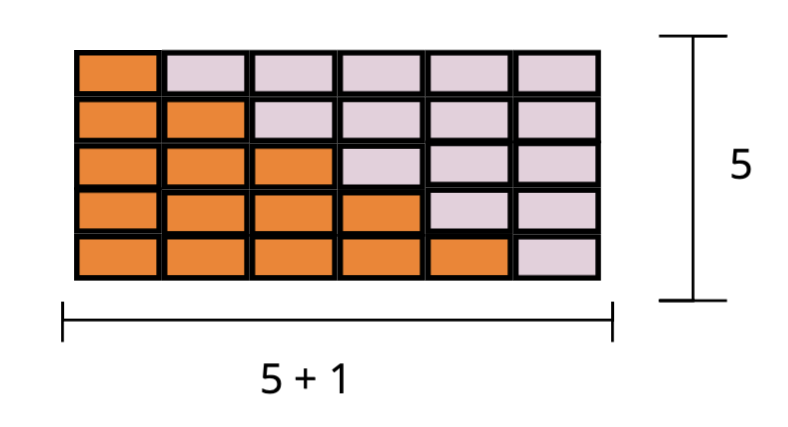
Combien de briques avons-nous au total? Il s’agit simplement de la surface du rectangle entier, qui est $5\times 6=30$.

Nous avons des $n$ lignes et des $n+1$ colonnes, puisque chaque brique orange est associée à une brique blanche.

Mais bien sûr, nous ne voulons pas la quantité totale de briques, nous voulons seulement le nombre de briques orange, qui n’est rien d’autre que la moitié des briques au total, dans notre exemple $30\&diviser;2=15$.

La validité de cette formule peut être démontrée à l’aide d’un exemple générique, où l’axe $y$ a une longueur $n$ et l’axe $x$ a une longueur $n+1$. La quantité de carrés noirs représente la somme des premiers $n$ entiers.

Utilisez le curseur ci-dessous pour le tester pour différentes valeurs de $n$.

Les mathématiques à l’œuvre

La formule de sommation de Gauss peut être formellement écrite comme suit :