Séquence de Fibonacci

Une séquence est une liste de nombres ou d’objets dans un certain ordre, où la répétition est autorisée. Les séquences sont dites finies si elles ont un nombre limité d’objets et infinies dans le cas contraire.

Examples:

• {1, 2, 3, 4, …} - est une infinite suite d’entiers naturels
• {2, 4, 6, 8, 10} - est une finite suite des cinq premiers nombre pairs
• {Z, Y, X, W, V} - est une finite suite de les cinq dernières lettres de l’alphabet anglais.
• {X, O, X, O, …} - est une infinite séquence de X et O dans un ordre alterné.

Comment la suite de Fibonacci est-elle définie ?

La séquence de Fibonacci est une suite de nombres, où chaque nombre est déterminé comme la somme des deux précédents. Cette séquence commence généralement par 0 et 1 (les exemples suivants sont également basés sur ce principe), bien qu’il y ait d’autres modifications.
Une telle séquence commencerait par 0, 1, 1, 2, 3, 5, 8, 13… et se poursuivrait ainsi à l’infini.

Les nombres de Fibonacci ont été mentionnés par des mathématiciens indiens dès 200 avant J.-C., mais c’est Léonard de Pise qui les a introduits pour la première fois dans les mathématiques occidentales au 13e siècle.

Les nombres de Fibonacci apparaissent très souvent dans le monde naturel. Le nombre de pétales d’une fleur, les têtes de graines, les coquillages et même les ouragans suivent souvent des schémas conformes aux nombres de Fibonacci. Cette célèbre séquence trouve des applications dans de nombreux départements, de l’informatique à la photographie, où elle est également fortement corrélée à ce que l’on appelle le “nombre de Fibonacci”. fortement corrélée à ce que nous appelons le nombre d’or.

Les nombres de Fibonacci sont à l’origine de nombreux modèles numériques magnifiques.

Comment comprendre visuellement ces nombres

Commençons par placer deux $1\times 1$ carrés l’un à côté de l’autre.

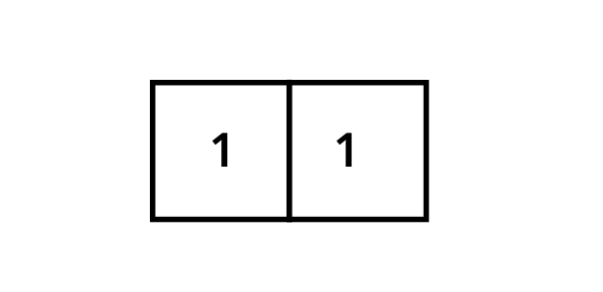
Nous obtenons ainsi un $1\times 2$ rectangle. En dessous, plaçons un $2\times 2$ carré pour que les longueurs des côtés adjacents correspondent.

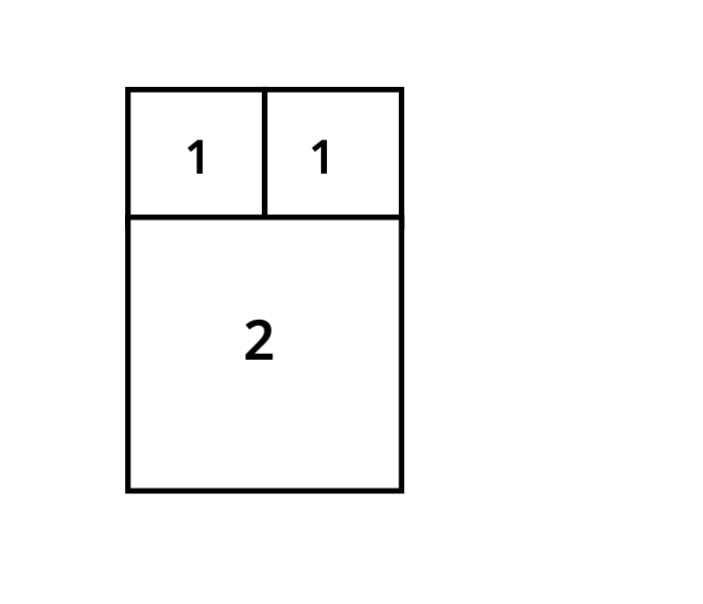
Et à côté, un $3\time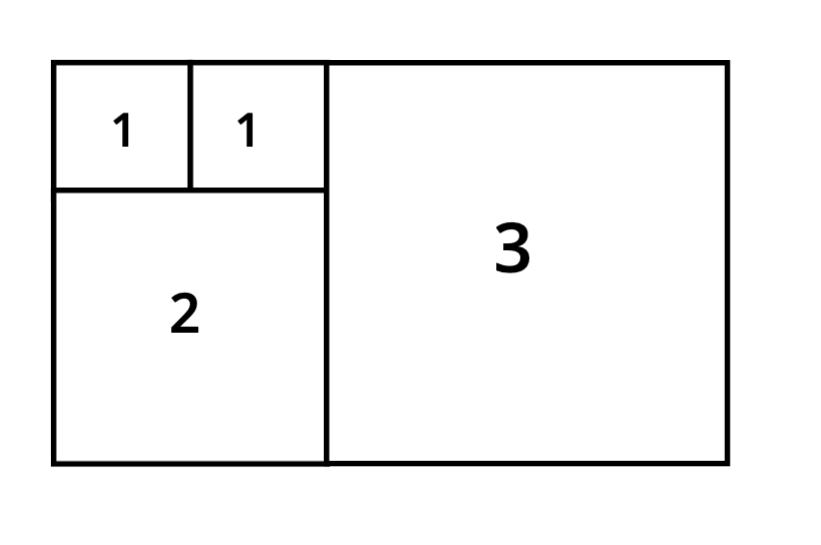s 3$ carré En dessous, un $5\time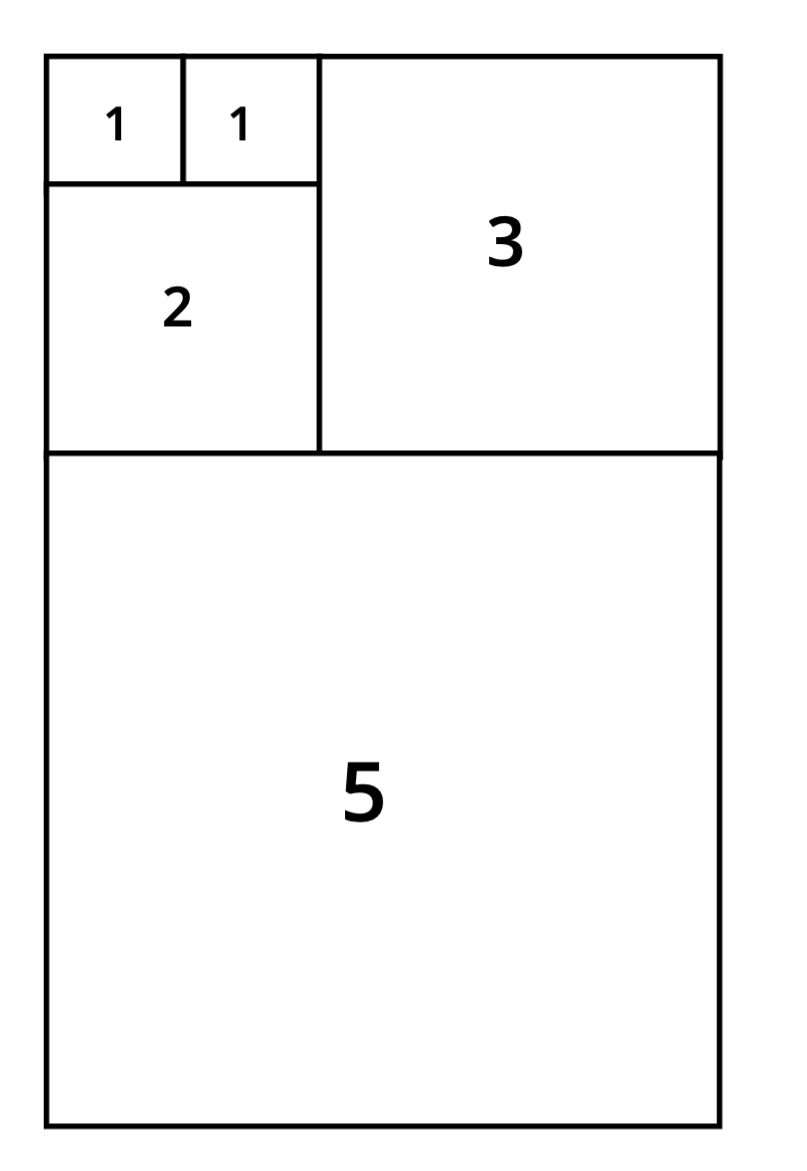s 5$ carré Nous avons maintenant créé un rectangle géant. Laissez-moi maintenant vous poser une question:

Quelle est l’aire du rectangle final ?

La réponse la plus triviale serait la somme des aires de tous les carrés à l’intérieur du rectangle. Mais comme il s’agit d’un rectangle Mais comme il s’agit d’un rectangle, nous pouvons également multiplier la base et la hauteur pour obtenir l’aire totale, qui serait la suivante $5\times (5+3)=5\times 8$ , le 8 étant également le prochain nombre de Fibonacci de la séquence.

Si nous continuons ainsi, nous générerons des rectangles des formes suivantes :

• $8\times 13$
• $13\times 21$
• $21\times 34$
• $34\times 55$
• $55\times 89$

En divisant la longueur du côté le plus grand par la longueur du côté le plus petit, on obtient:

• $13÷8=1.625$
• $21÷13=1.615$
• $34÷21=1.619$
• $55÷34=1.6176$
• $89÷55=1.61818$

Au fur et à mesure que nous avançons, nous nous rapprochons de 1,618034… connu par beaucoup comme le nombre d’or.

Essayez vous-même

Utilisez la barre de défilement ci-dessous pour découvrir comment le motif s’agrandit avec l’ajout de carrés.

Les mathématiques à l’œuvre

La formule utilisée pour générer une telle séquence est la suivante

et

pour $n>1$.