Gaußsche Summenformel

Carl Friedrich Gauß (1777-1855 n. Chr.) gilt als einer der einflussreichsten Mathematiker aller Zeiten. Er revolutionierte nicht nur das Feld der Mathematik, sondern darüber hinaus auch Physik und Statistik. Er besaß bereits in sehr jungen Jahren eine starke mathematische Intuition. Der Legende nach wurde der junge Carl als Schuljunge von seinem Lehrer aufgefordert, die Zahlen von 1 bis 100 zusammenzuaddieren - und dabei entdeckte er ein Muster! Aus den 100 Zahlen formte er 50 Paare - die erste und letzte Zahl, die zweite und vorletzte Zahl, und so weiter - und addierte diese zusammen. Jedes dieser Paare ergibt in Summe 101: 1+100 = 2+99 = 3+98 = … = 50+51 = 101. Demnach war die Summe einfach $50\times 101=5050$.

Malen wir ein Bild!

Fangen wir an uns vorzustellen, dass wir die Summe der ersten fünf natürlichen Zahlen bestimmen wollen, also 1 + 2 + 3 + 4 + 5. Anstatt einfach Zahlen aufschreiben, tun wir so als wären wir Bauarbeiter die eine Treppe bauen. Die erste Stufe braucht einen Stein, die zweite zwei, und so weiter bis zur fünften Stufe, die fünf Steine benötigt. Das ganze sieht dann in etwa so aus:

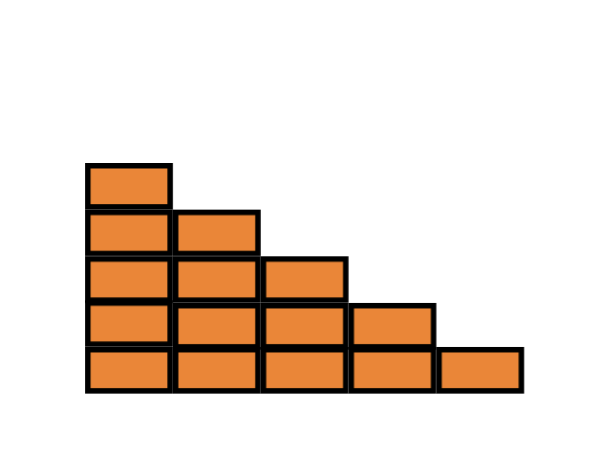
Wir könnten die Treppe jetzt bis zu 100 oder sogar 1000 Stufen ausbauen, aber für die Idee reichen erstmal fünf. Wie können wir jetzt die Steine in dieser Treppe bestimmen? Unsere erste Idee ist einfach die Steine in der Treppe zu zählen - aber es geht noch einfacher! Bauen wir dazu noch eine gespiegelte Treppe (in einer anderen Farbe, um die beiden Treppen voneinander zu unterscheiden),

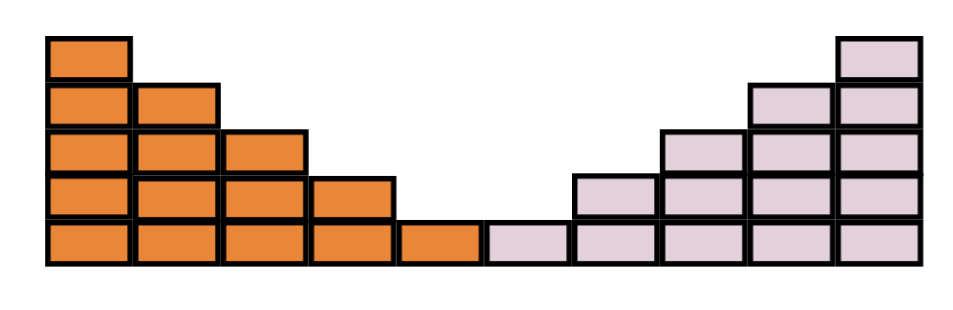
und jetzt kippen wir diese gespiegelte Treppe um.

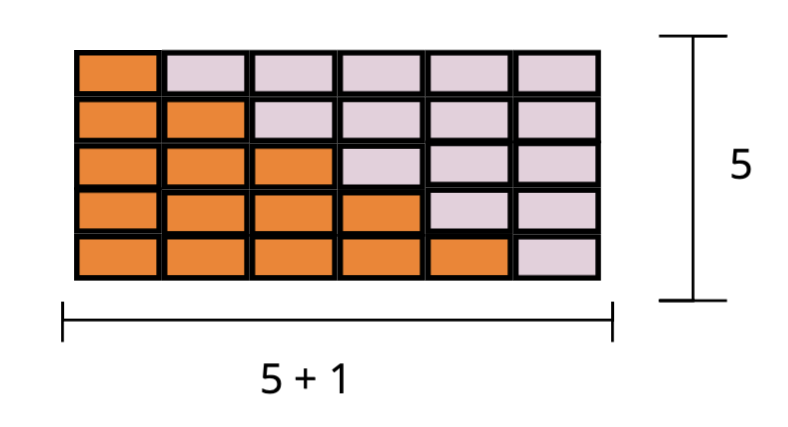
Wie viele Steine haben wir jetzt insgesamt? Die beiden Treppen ergeben zusammen ein vollständiges Rechteck, welches aus $5\times 6=30$ Steinen besteht.

Wenn unsere Treppe also aus $n$ Stufen besteht, hat unser Rechteck $n$ Zeilen und $n+1$ Spalten, weil die orangenen Blöcke jeweils mit der ergänzenden Anzahl weißen Blöcken gepaart ist.

Aber natürlich wollen wir nicht die gesamte Anzahl an Steinen, sondern nur die Anzahl der orangenen Steine. Aber das ist einfach die Hälfte, da die orangene und die gespiegelte weiße Treppe gleich viele Steine besitzen. In unserem Beispiel sind es also $30÷2=15$ orangene Steine.

Wir können nun sehen, dass der Satz für eine beliebige Zahl Stufen gilt: Eine schwarze und eine weiße Treppe mit jeweils $n$ Stufen ergeben zusammen ein Rechteck mit Höhe $n$ und Breite $n+1$. Die Anzahl der schwarzen Blöcke ist gleich der Summe der ersten $n$ natürlichen Zahlen.

Benutze den Schieber um verschiedene Werte für $n$ auszuprobieren.

Die Mathematik dahinter

Die Gaußsche Summenformel für die Summe der ersten $n$ natürlichen Zahlen lautet