Fibonacci-Folge

Eine Folge ist eine Liste von Zahlen oder Objekten in einer bestimmten Reihenfolge, wobei Wiederholungen von Objekten erlaubt sind. Wir nennen Folgen endlich, wenn sie eine endliche Anzahl an Objekten umfassen. Sonst nennen wir sie unendlich.

Beispiele:

• {1, 2, 3, 4,…} - ist eine unendliche Folge der natürlichen Zahlen.
• {2, 4, 6, 8, 10} - ist eine endliche Folge der ersten fünf positiven geraden Zahlen.
• {Z, Y, X, W, V} - ist eine endliche Folge der letzten fünf Buchstaben des Alphabets.
• {X, O, X, O,…} - ist eine unendliche Folge, die zwischen X und O alterniert.

Was ist die Fibonacci-Folge?

Die Fibonacci-Folge ist eine Folge von Zahlen, wobei jedes Element als die Summe seiner beiden Vorgänger definiert ist. Normalerweise definieren wir die ersten beiden Elemente der Folge als 0 und 1, aber auch andere Starts sind möglich. Eine Folge mit diesem Anfang sähe wie folgt aus: 0, 1, 1, 2, 3, 5, 8, 13, …

Die Fibonacci-Zahlen wurden von indischen Mathematikern bereits 200 v. Chr. entdeckt, aber zum ersten Mal vom italienischen Mathematiker Leonardo von Pisa (1170-1240 n. Chr.) im 13. Jahrhundert eingeführt.

Die Fibonacci-Folge erscheint in der Natur sehr häufig. Die Blüten von Blumen, Fruchständen von Pflanzen, Muscheln oder Orkane folgen dem Muster der Fibonacci-Zahlen. Anwendung findet diese berühmte Folge in verschiedensten Bereichen von Computerwissenschaften bis zu Fotografie, wo sie eng mit dem Phänomen des Goldenen Schnitts zusammenhängt.

Tausende von bezaubernden Mustern ergeben sich durch die Fibonacci-Folge.

Wie können wir die Fibonacci-Folge visuell verstehen?

Beginnen wir mit zwei $1\times 1$-Quadraten nebeneinander.

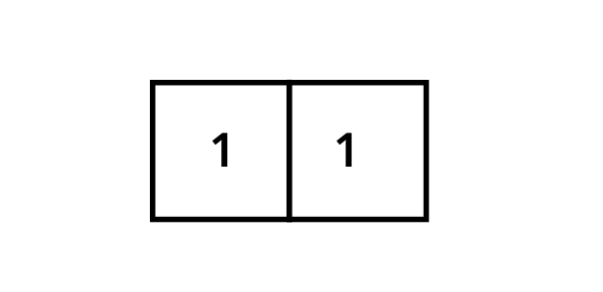
Zusammen ergeben diese ein $1\times 2$-Rechteck. Bauen wir nun unterhalb ein $2\times 2$-Quadrat an.

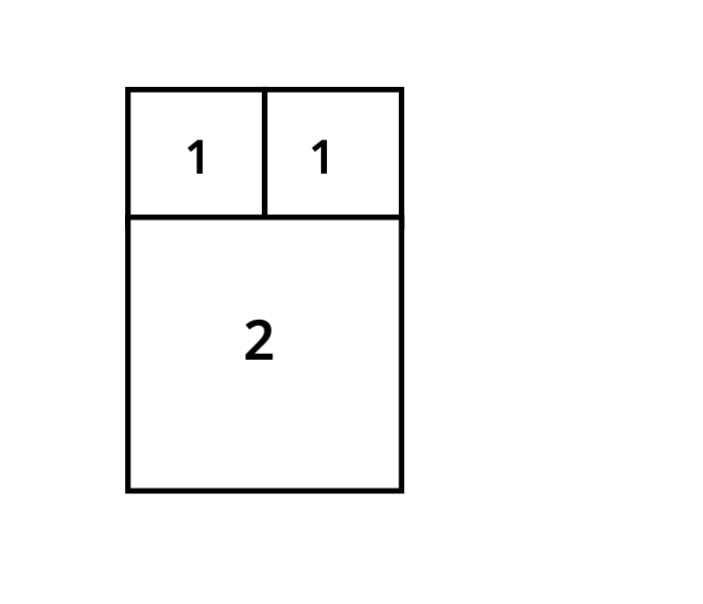
Neben dieses Gebilde kommt nun, entsprechend der Höhe, ein $3\times 3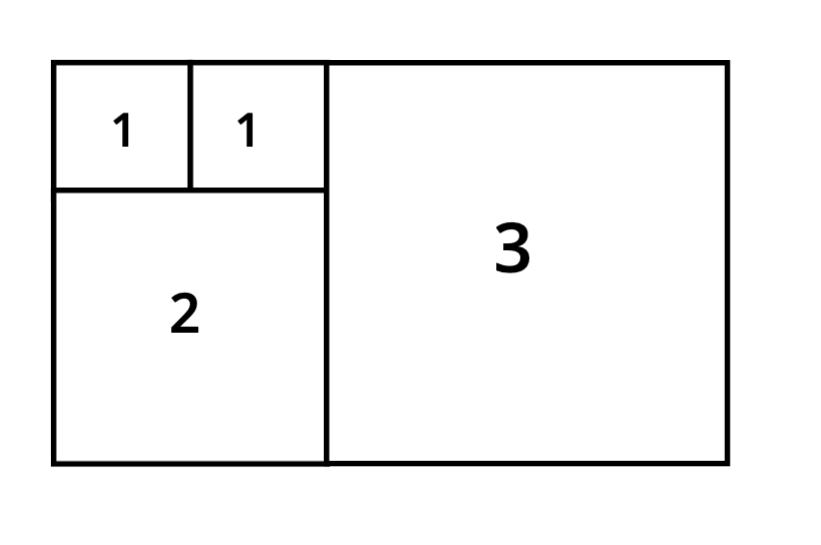$-Quadrat. Darunter fügen wir als nächstes ein $5\times 5$-Quadrat hinzu. 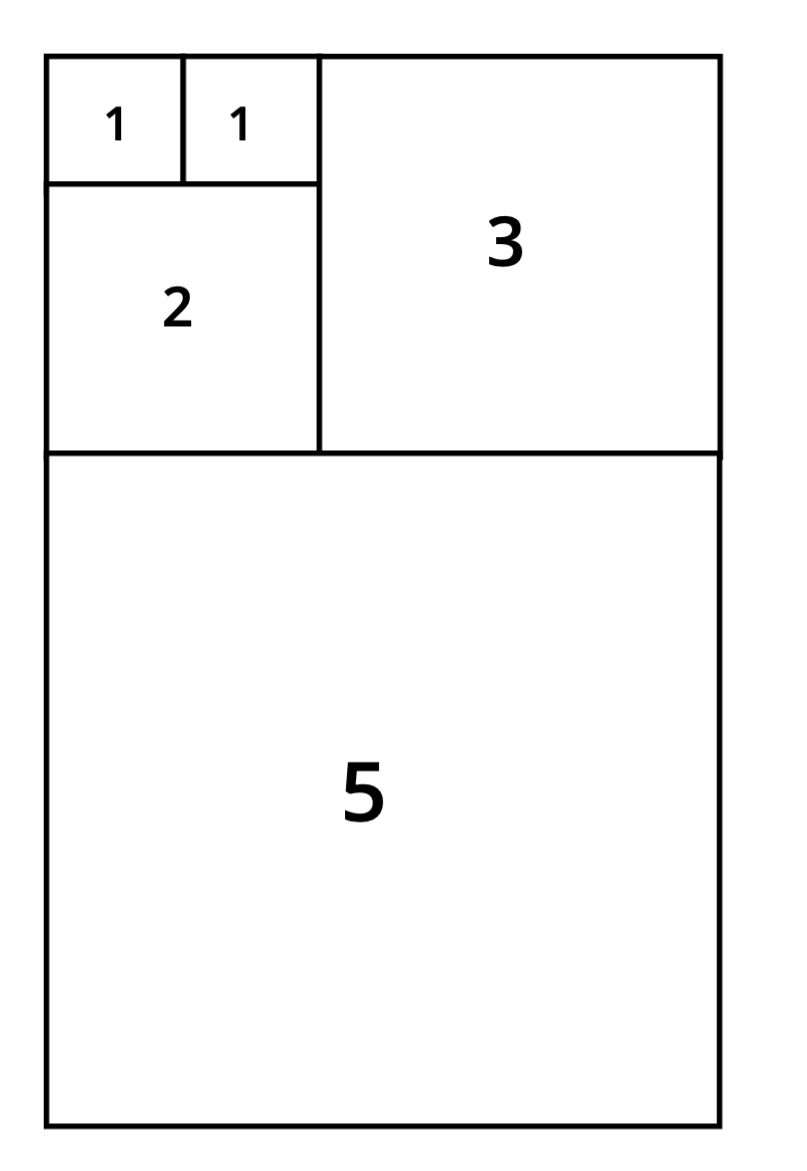Zusammen ergibt dies ein gigantisches Rechteck. Nun die Frage:

Was ist die Fläche dieses Rechtecks?

Die offensichtlichste Antwort ist einfach die Flächen all dieser Quadrate zusammenzuaddieren. Aber da die finale Form ein Rechteck ist, können wir auch einfach seine Breite mit siner Höhe multiplizieren um die Fläche zu bestimmen: $5\times (5+3)=5\times 8$, wobei 8 auch die nächste Zahl in der Fibonacci-Folge ist.

Wenn wir so weitermachen erhalten wir Rechtecke der folgenden Größen:

• $8\times 13$
• $13\times 21$
• $21\times 34$
• $34\times 55$
• $55\times 89$

Wenn wir nun die längere Seitelänge des Rechtecks durch die kürzere dividieren, erhalten wir

• $13÷8=\mathrm{1,625}$
• $21÷13=\mathrm{1,615}$
• $34÷21=\mathrm{1,619}$
• $55÷34=\mathrm{1,6176}$
• $89÷55=\mathrm{1,61818}$

Je größer unsere Rechtecke werden, desto näher kommen wir einem Wert von rund 1,618034…, der auch als goldener Schnitt bekannt ist.

Versuch es selbst

Nutze den Schieber und untersuche wie das Rechteck anwächst.

Die Mathematik dahinter

Die Formeln, um die Fibonacci-Folge zu generieren, lauten

und

für $n>1$.