Gauss Summation

Carl Friedrich Gauss (1777-1855 AD) is acknowledged as one of the most influential mathematicians of all time. He contributed not only to the field of mathematics, but physics and statistics as well. His strong numerical intuition was already noticed at an early age, when he was tasked by his teacher to sum up the numbers from one to a hundred. Here, he recognized a pattern. He had fifty pairs of numbers when he added the first and last number in the series, the second and second-last number in the series, and so on. For example: (1 + 100), (2 + 99), (3 + 98), …, (50 + 51), and each pair has a sum of 101. So $50\times 101=5050$.

How to prove sum of naturals visually

Let’s imagine we want to know the sum of the first five natural numbers. That means we have to add 1 + 2 + 3 + 4 + 5. Instead of writing out numbers, let’s pretend we are construction workers, and we are building a pair of stairs of identically coloured bricks. We want to layer 1 brick on top of, 2 bricks, 3 bricks, all the way down to 5 bricks. Something like this:

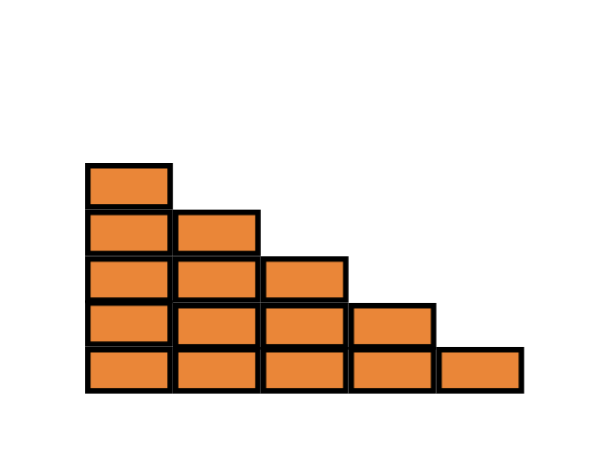
We could go to 100 or 1000 bricks, but 5 bricks are enough to get the idea. How do we count the number of the bricks needed to construct the stairs? Of course, we could do it manually but why do that where there’s another quicker way! Let’s say we mirror our stairs (using another colour to represent the mirrored bricks),

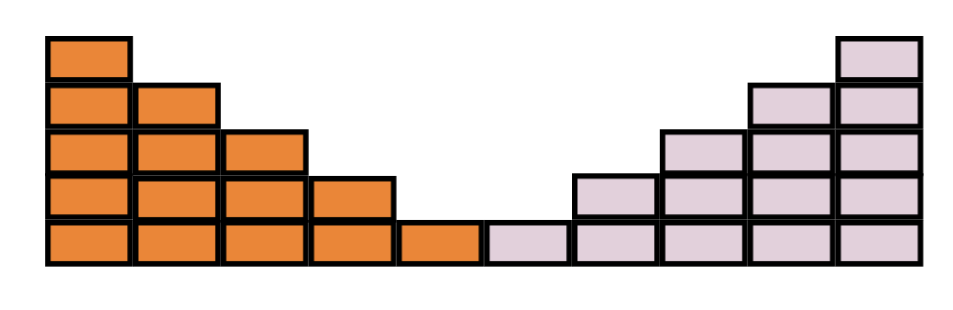
and then topple it over:

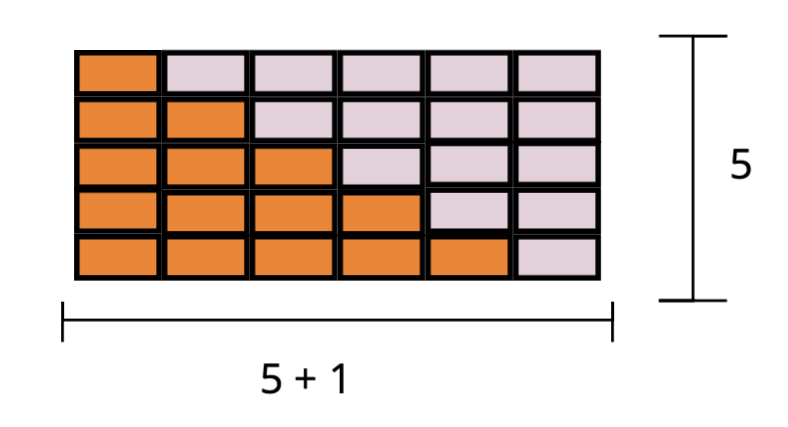
How many bricks do we have in total? Well that’s just the area of the whole rectangle, which is $5\times 6=30$.

We have $n$ rows and $n+1$ columns, since every orange bricked is paired up with a white one.

But of course, we don’t want the total amount of bricks, we just want the number of orange bricks, which is nothing else but the half of the bricks in total, in our example $30÷2=15$.

That this formula holds can be shown with a generic example, where the $y$-axis has length $n$ and $x$-axis has length $n+1$. The amount of the black squares represents the sum of the first $n$ integers.

Use the slider below to test it for different values of $n$.

The math behind it

The Gauss summation formula can be formally written like this: