Fibonacci Sequence

A sequence is a list of numbers or objects that are in a certain order, where repetition is allowed. Sequences are called finite, if they have a limited number of objects and otherwise infinite.

Examples:

• {1, 2, 3, 4, …} - is an infinite sequence of the natural numbers
• {2, 4, 6, 8, 10} - is a finite sequence of the first five even numbers
• {Z, Y, X, W, V} - is a finite sequence of the last five letters of the english alphabet.
• {X, O, X, O, …} - is an infinite sequence of X and O in an alternating order.

How is Fibonacci’s sequence defined

The Fibonacci sequence is a sequence of numbers, where each number is determined as the sum of the two preceding ones. This sequence typically starts from 0 and 1 (the examples in the following are also based on this), although there are other alterations.
Such a sequence would start with 0, 1, 1, 2, 3, 5, 8, 13… and then continue in this manner forever.

The Fibonacci numbers were mentioned by Indian mathematicians way back in 200 BC, but were first properly introduced to the Western mathematics by Leonardo of Pisa in the 13th century.

In the natural world the Fibonacci numbers appear very often. The number of petals in a flower, seed heads, shells and even hurricanes often follow patterns according to the Fibonacci numbers. This famous sequence finds application in many departments from computer science to photography, where it’s also strongly correlated to what we know as the golden ratio.

There are many beautiful number patterns that emerge from the Fibonacci numbers.

How to visually understand these numbers

Let’s start by putting two $1\times 1$ squares next to one another.

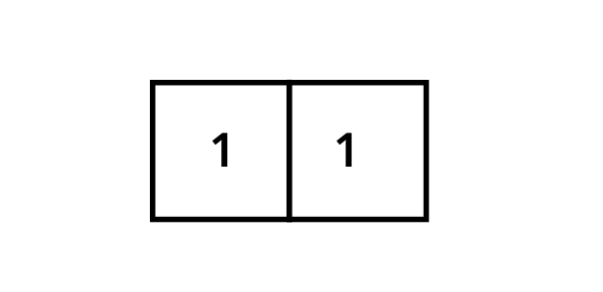
As a result we get a $1\times 2$ rectangle. Beneath that let’s put a $2\times 2$ square so that the lengths of the adjacent sides match.

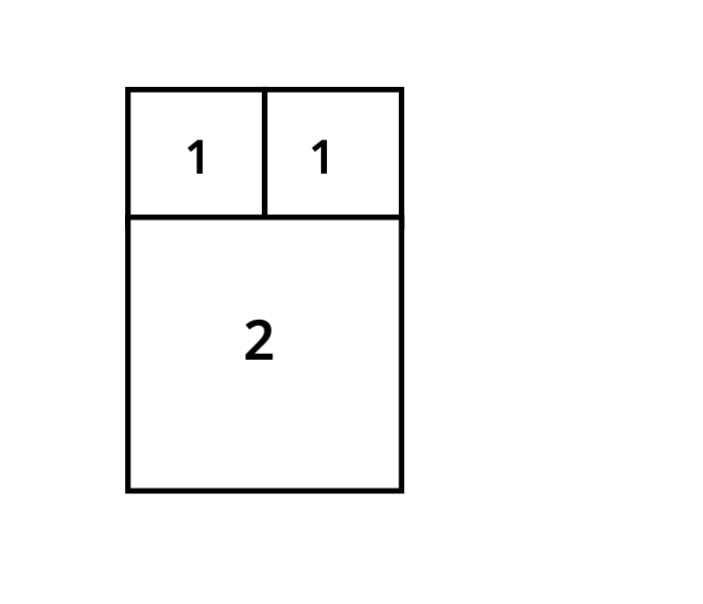
And next to that, a $3\times 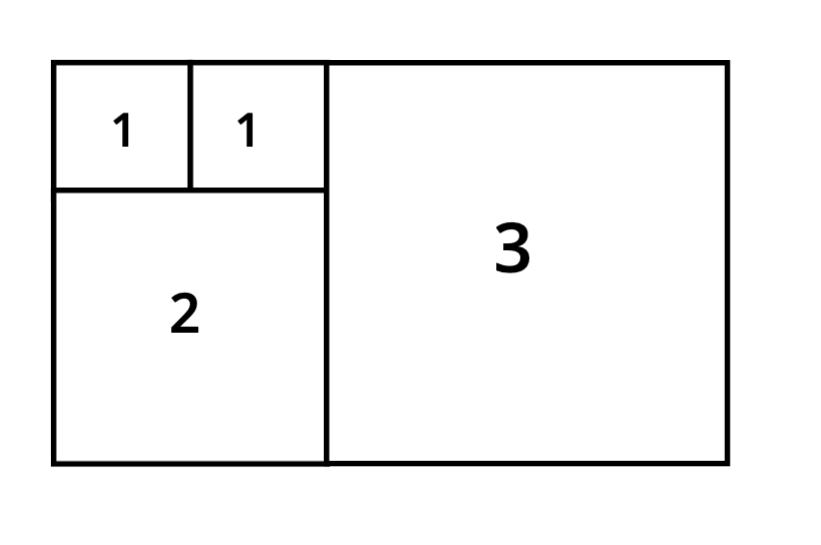3$ square Beneath that a $5\times 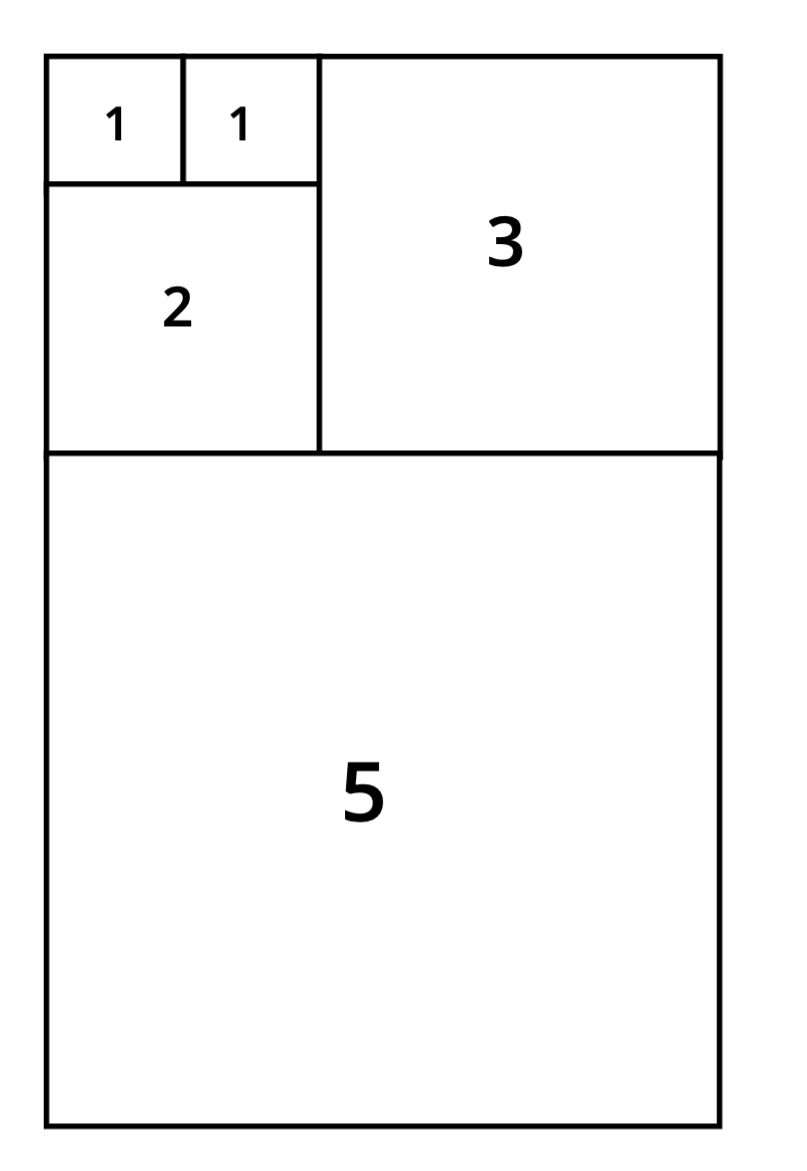5$ square We have now created one giant rectangle. Now let me ask you a question:

What’s the area of the final rectangle?

The most trivial answer would be the sum of the areas of all the squares inside it. But since it is a rectangle we can also multiply base and height to get the total area which would be $5\times (5+3)=5\times 8$ , with 8 also being the next Fibonacci number on the sequence.

If we continue like this we will be generating rectangles of the following forms:

• $8\times 13$
• $13\times 21$
• $21\times 34$
• $34\times 55$
• $55\times 89$

Now check this out, by dividing the bigger side length by the smaller one we get:

• $13÷8=1.625$
• $21÷13=1.615$
• $34÷21=1.619$
• $55÷34=1.6176$
• $89÷55=1.61818$

As we continue, we get closer to about 1.618034… known to many people as the golden ratio.

Try it yourself

Use the slider below to explore how the pattern grows with more squares.

The math behind it

The formula used to generate such a sequence is

and

for $n>1$.