Théorème de Pythagore

Pythagore de Samos (570-495 av. J.-C.) était un philosophe grec très influent, dont les travaux ont contribué à de nombreux domaines tels que la musique, la philosophie, l’astronomie et les mathématiques. a contribué à de nombreux domaines tels que la musique, la philosophie, l’astronomie et les mathématiques, ces dernières incluant le célèbre théorème de Pythagore.

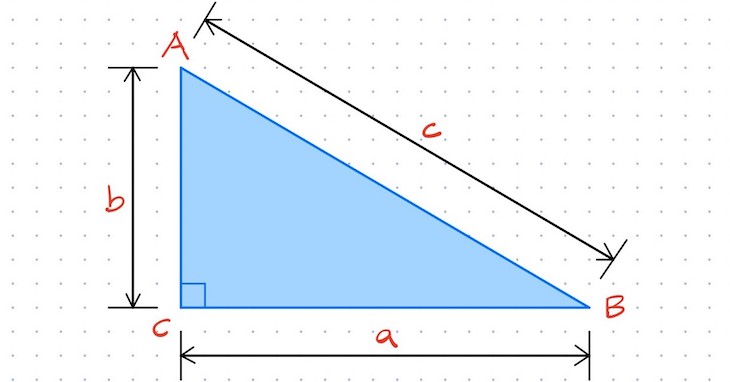
Le théorème de Pythagore est un théorème géométrique fondamental et certainement très connu. Selon ce théorème, dans un triangle rectangle (dont l’un des angles est de 90°), l’hypoténuse (le côté le plus long, qui se trouve à l’opposé de l’angle de 90°) est égale à la racine carrée de la somme des aires des carrés des deux autres côtés.

Ce théorème a de nombreuses applications, notamment dans les domaines de l’ingénierie et de la construction, de la reconnaissance faciale dans les caméras de sécurité, de la navigation et bien d’autres encore.

À prouver: Lorsqu’un triangle a un angle droit (90°) et que des carrés sont faits sur chacun des trois côtés, alors le plus grand carré a exactement la même surface que les deux autres carrés réunis !

Visualisons l’énoncé ci-dessus

Nous dessinons un triangle rectangle et à côté des côtés du triangle, nous dessinons des carrés :

• Un $3\times 3$ carré pour la hauteur (côté)
• Un $4\times 4$ carré pour la largeur (côté)
• Un $5\times 5$ carré pour l’hypoténuse.

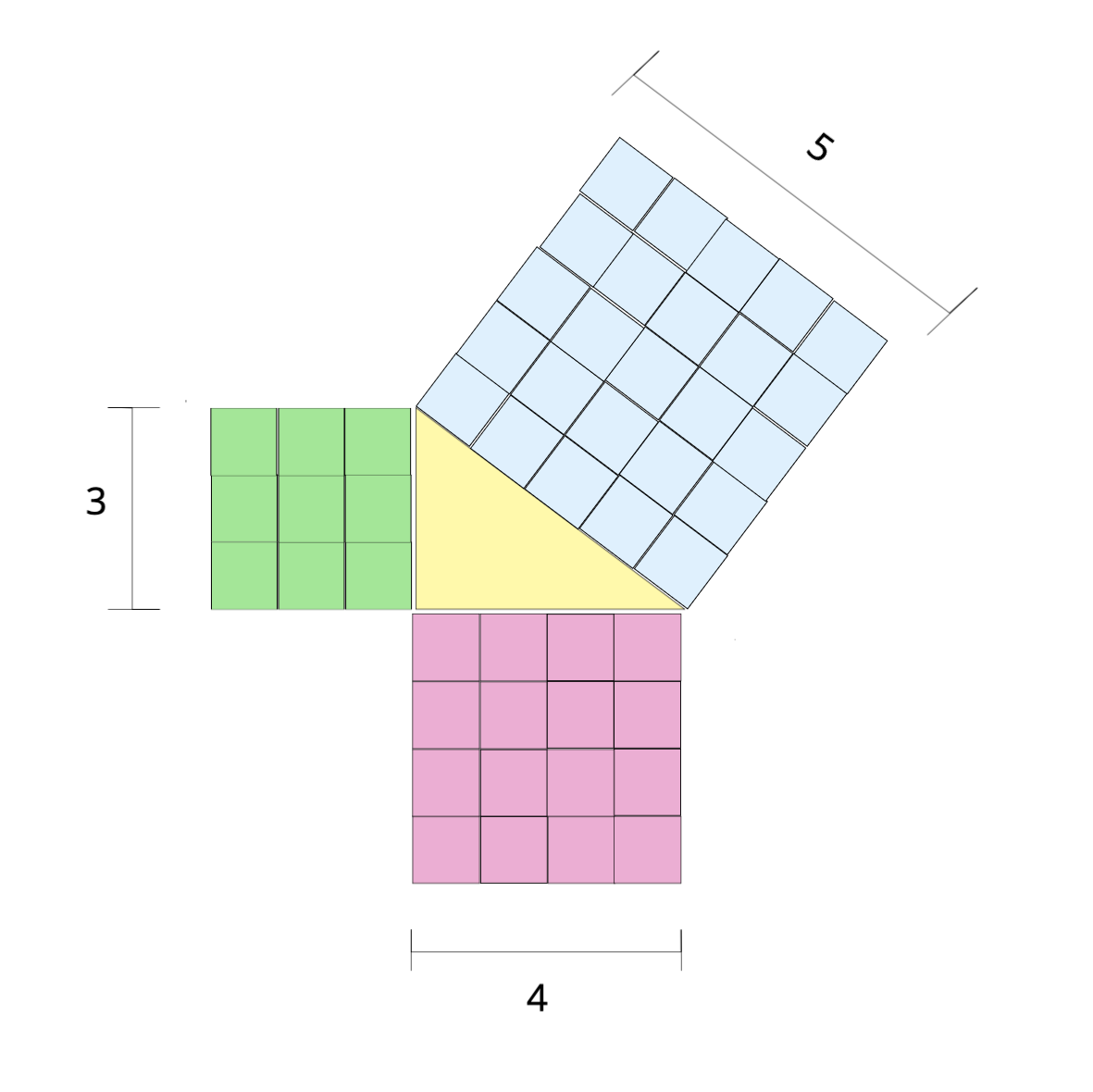
D’après le théorème, la somme des carrés des petits côtés doit être égale au carré de l’hypoténuse.

Est-ce le cas dans notre visualisation ?

Vérifions-le : Comptez les petits carrés des côtés, additionnez-les et comparez si la somme des côtés est égale à la somme des carrés de l’hypoténuse. Vous devriez obtenir 9 + 16 = 25.

Essayez vous-même

Joue avec $a$ et $b$ vérifier la validité de ce théorème. Voyez comment les formes s’emboîtent les unes dans les autres, ce qui montre que ces zones sont de taille égale.

Les mathématiques à l’œuvre

L’équation permettant d’exprimer le théorème dans un triangle rectangle est la suivante

où $a$ et $b$ représentent les cathéters, autrement dit les jambes adjacentes ou opposées de l’angle droit et $c$ est l’hypoténuse.