Pizza theorem

Hey, I brought something for us…

I’ve bought a pizza for us two to share! Who can do math with an empty stomach? Now, I only need to cut it into slices..

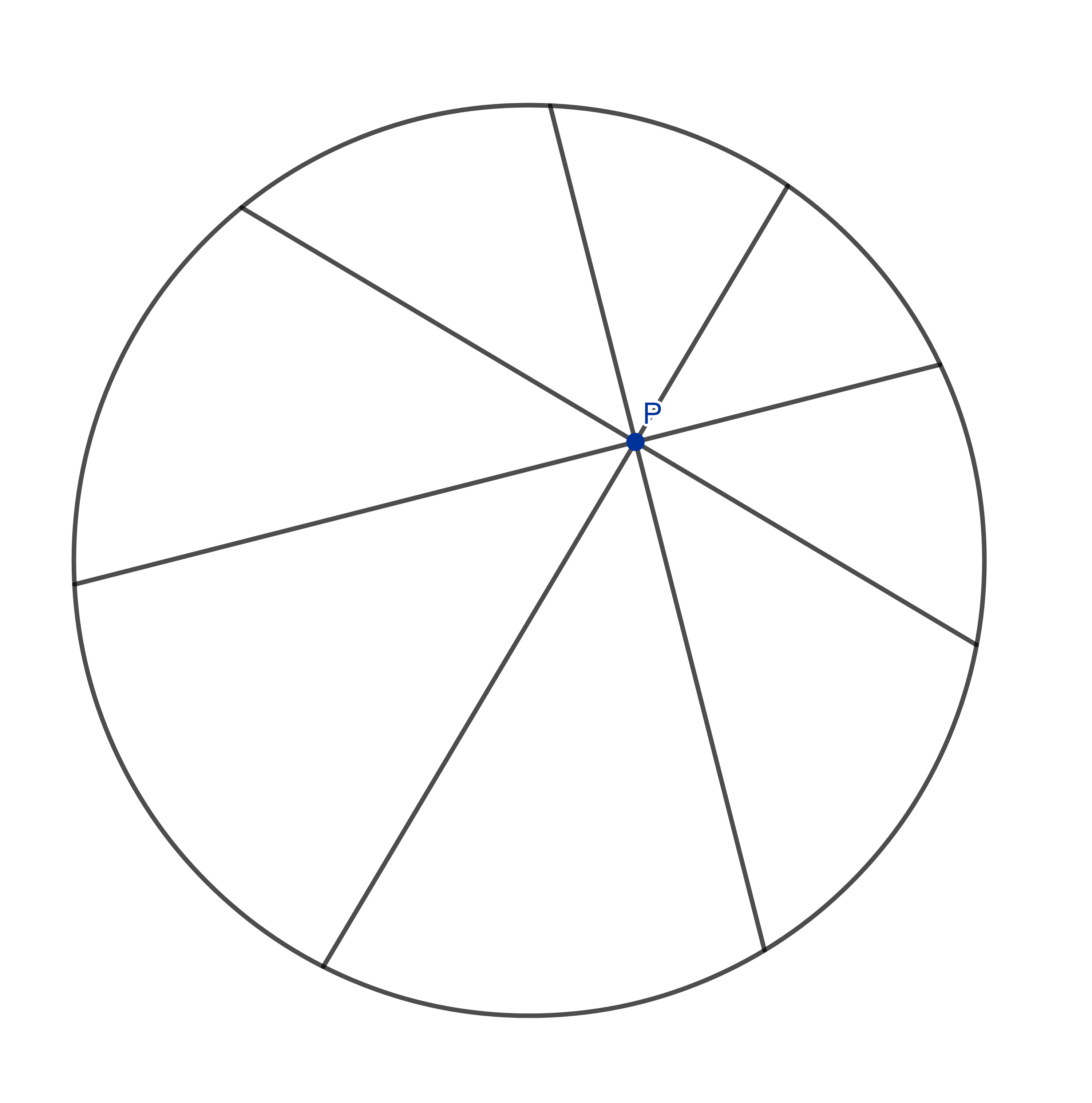
Oops. Now that doesn’t look nice at all! I made all the cuts nice and regular so that the eight angles between the cuts are equally spaced and form a 45° angle. But I didn’t hit the center of the pizza at all, so now all the slices look really weird. But don’t worry: If we go round the circle, you take every second slice and I take the rest, we will have exactly the same amount of pizza!

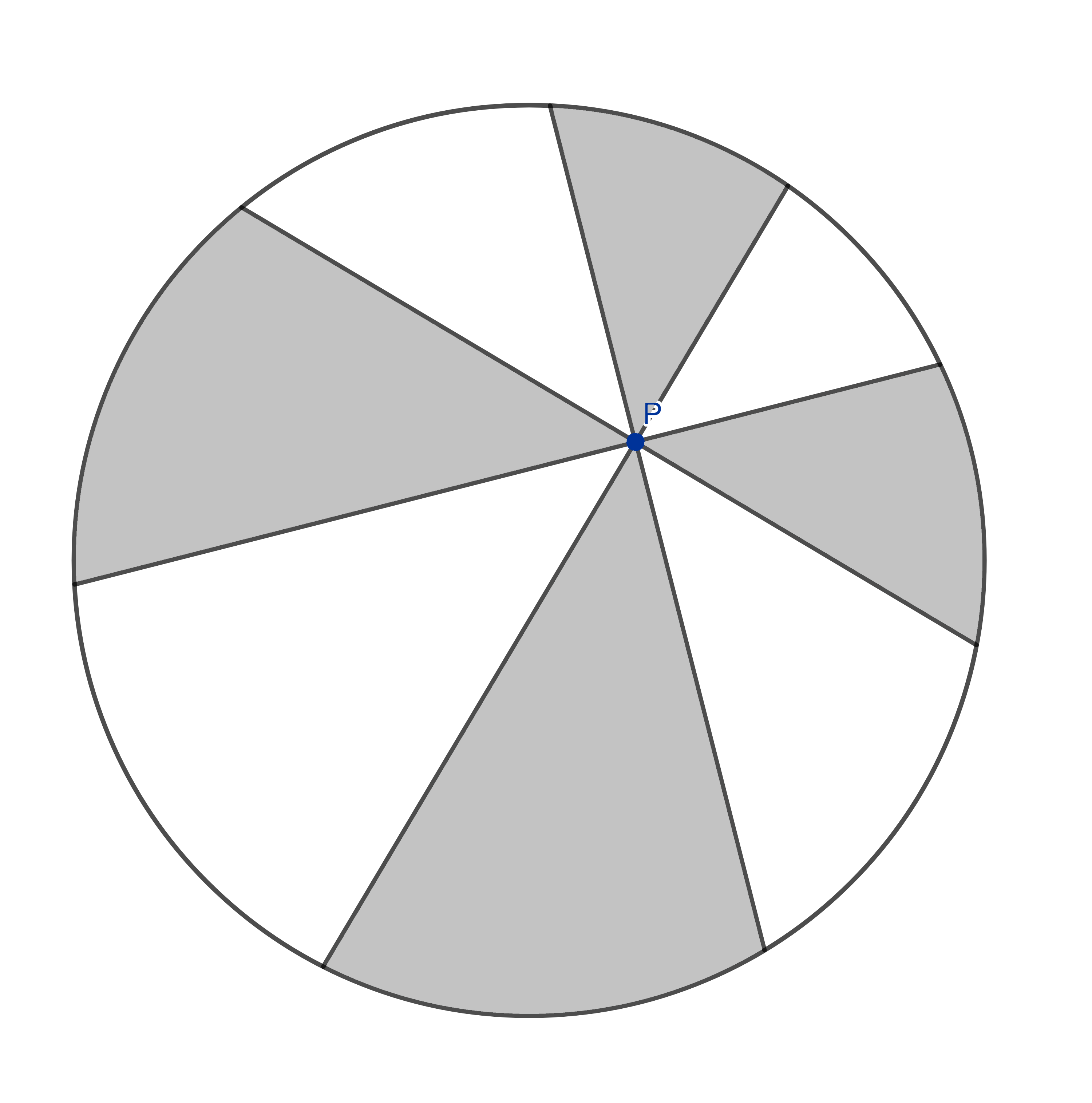
This is also known as the Pizza theorem. Who says math isn’t useful in the real world? And we will even prove it together!

Proving the pizza theorem

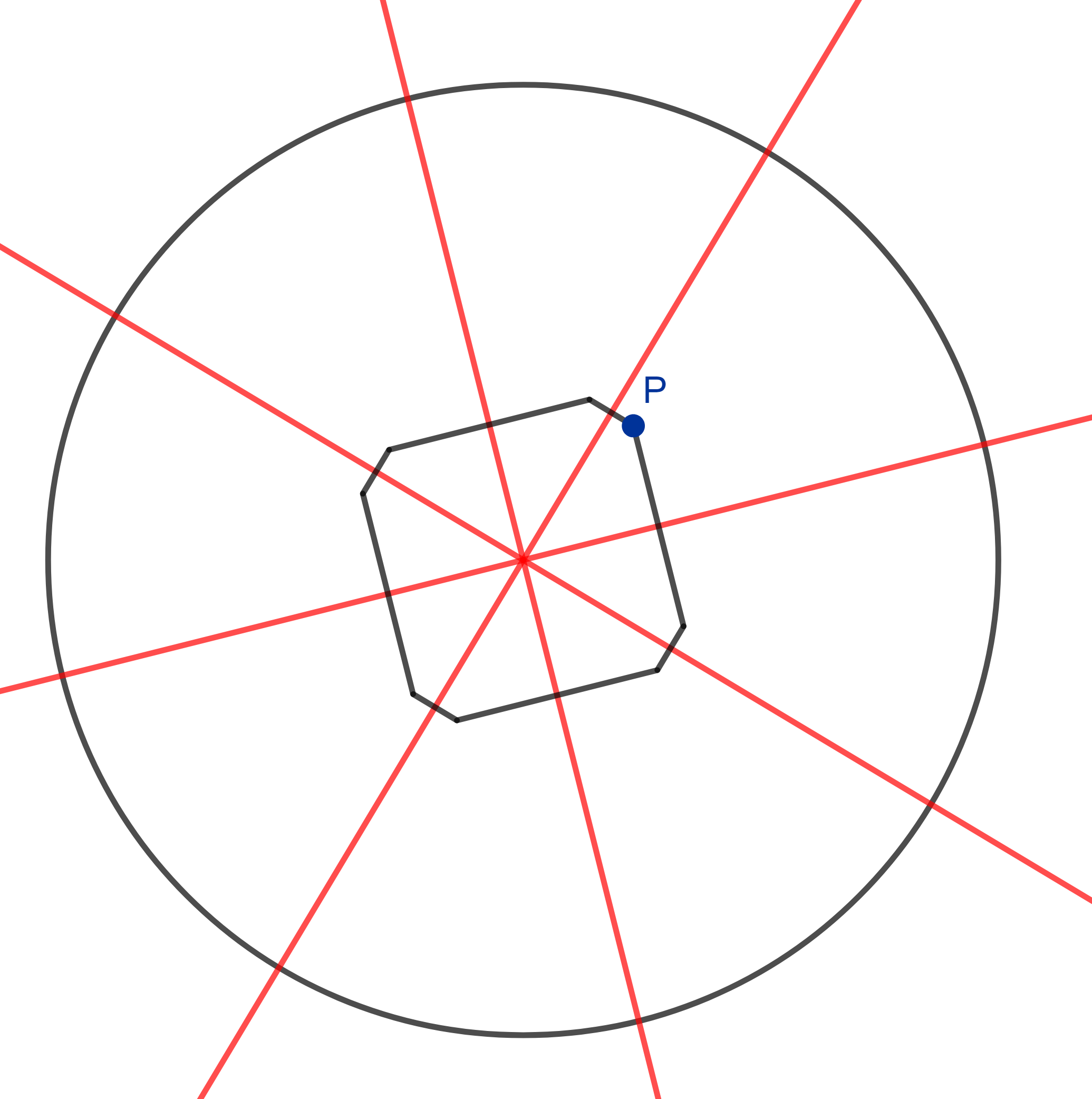
Now, how do we want to prove that your four slices together have the same area as my four slices? After all, they all look completely different. In these scenarios, it can be helpful to add a few more lines to your geometric construction - or cuts to your pizza - to create more shapes which clearly have the same area. We call two shapes congruent if they have the exact same form, size and area. A good way to create congruent shapes is by using symmetries, for example by mirroring some lines. That’s exactly what we are going to do! We take the cuts that we made and shift them to the center of the pizza (shown in red). Mirroring the cutting point along those lines give us an octagon (in black).

If we also mirror the cuts we have made earlier, we get the following cut-up pizza.

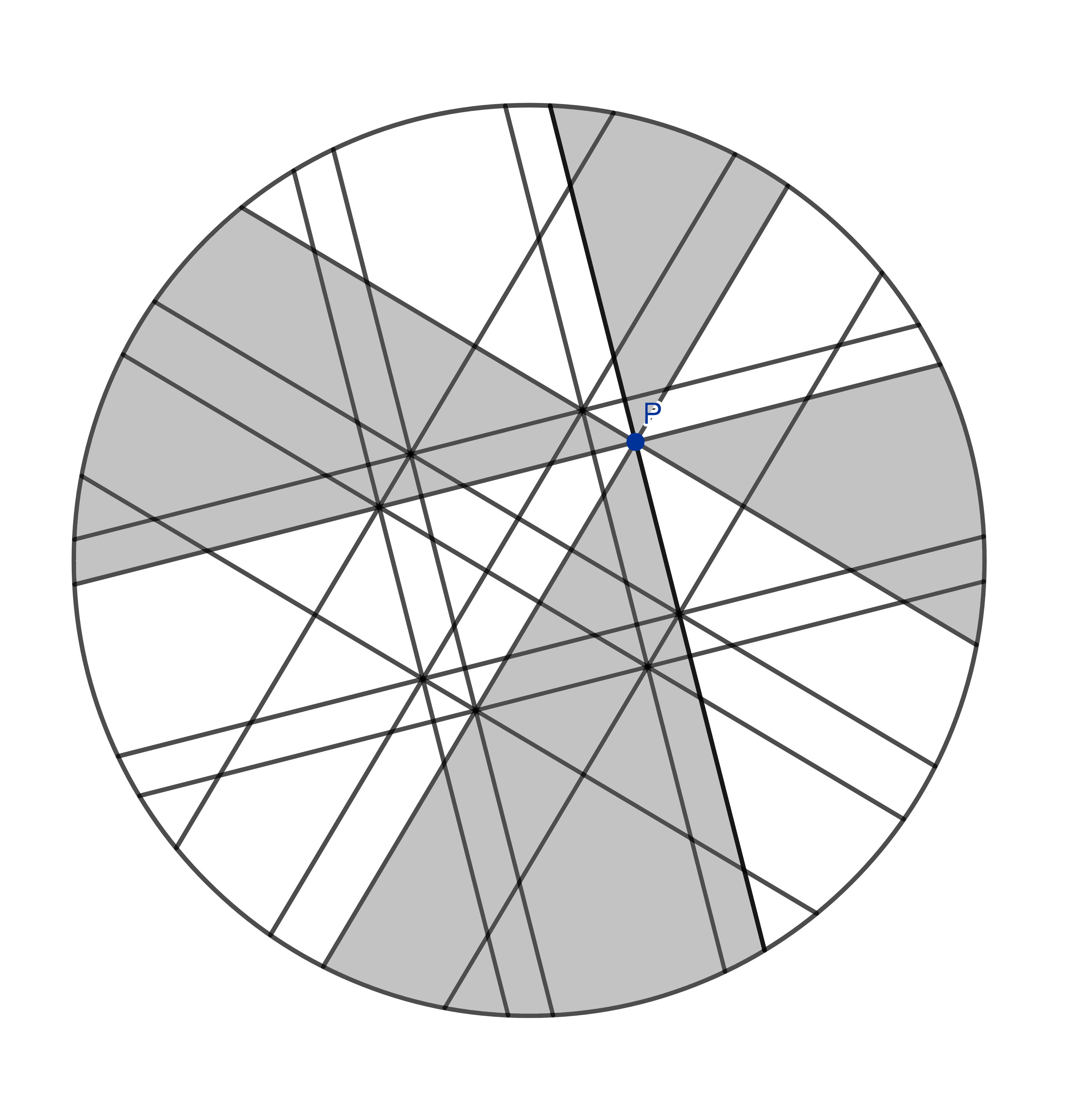
Don’t freak out! This looks very complicated but we will just concentrate on one mini-slice every time and find all the other mini-slices that look exactly like it. Let’s start with this one:

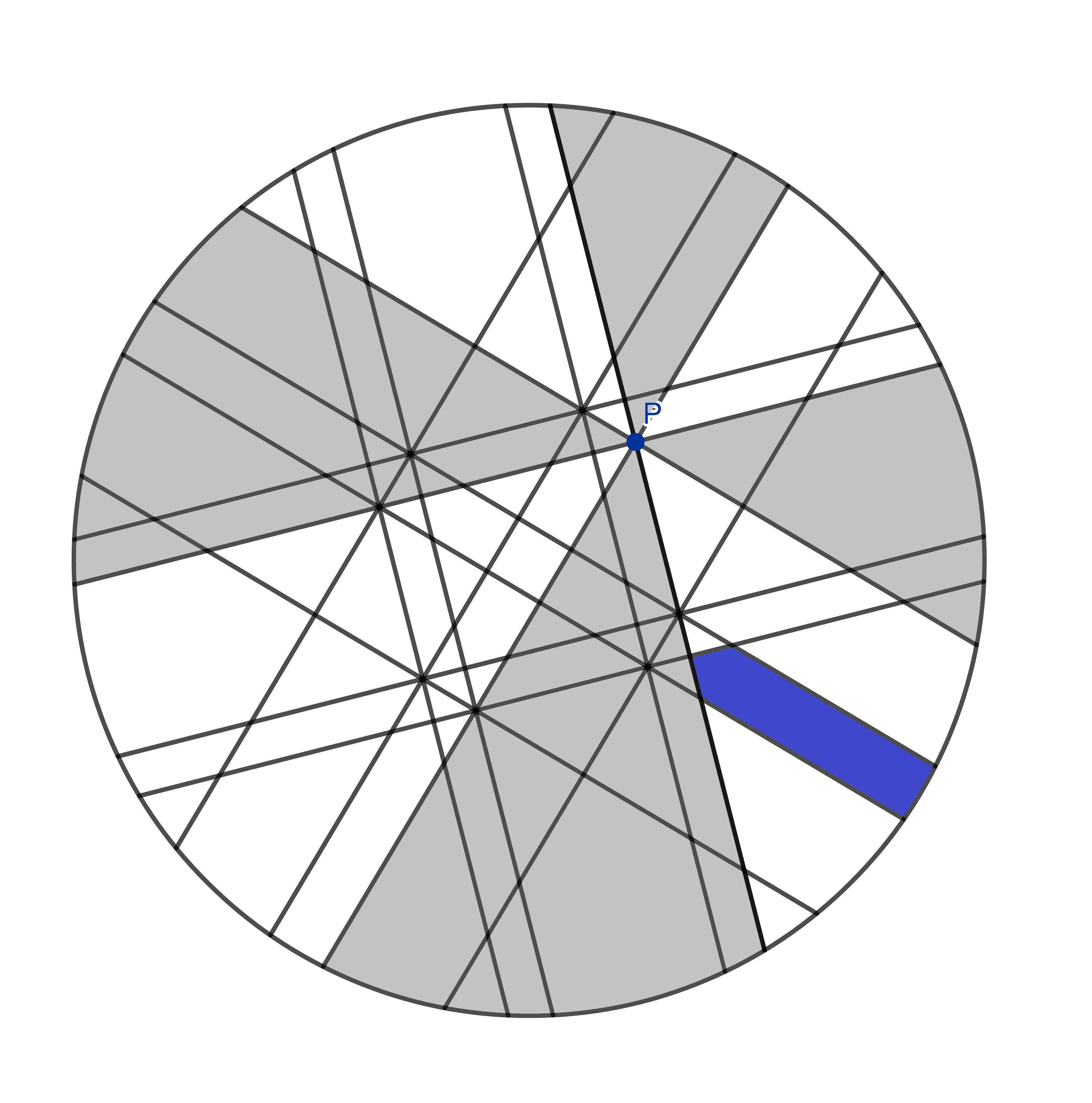
There are three more parts like it. Can you find them?

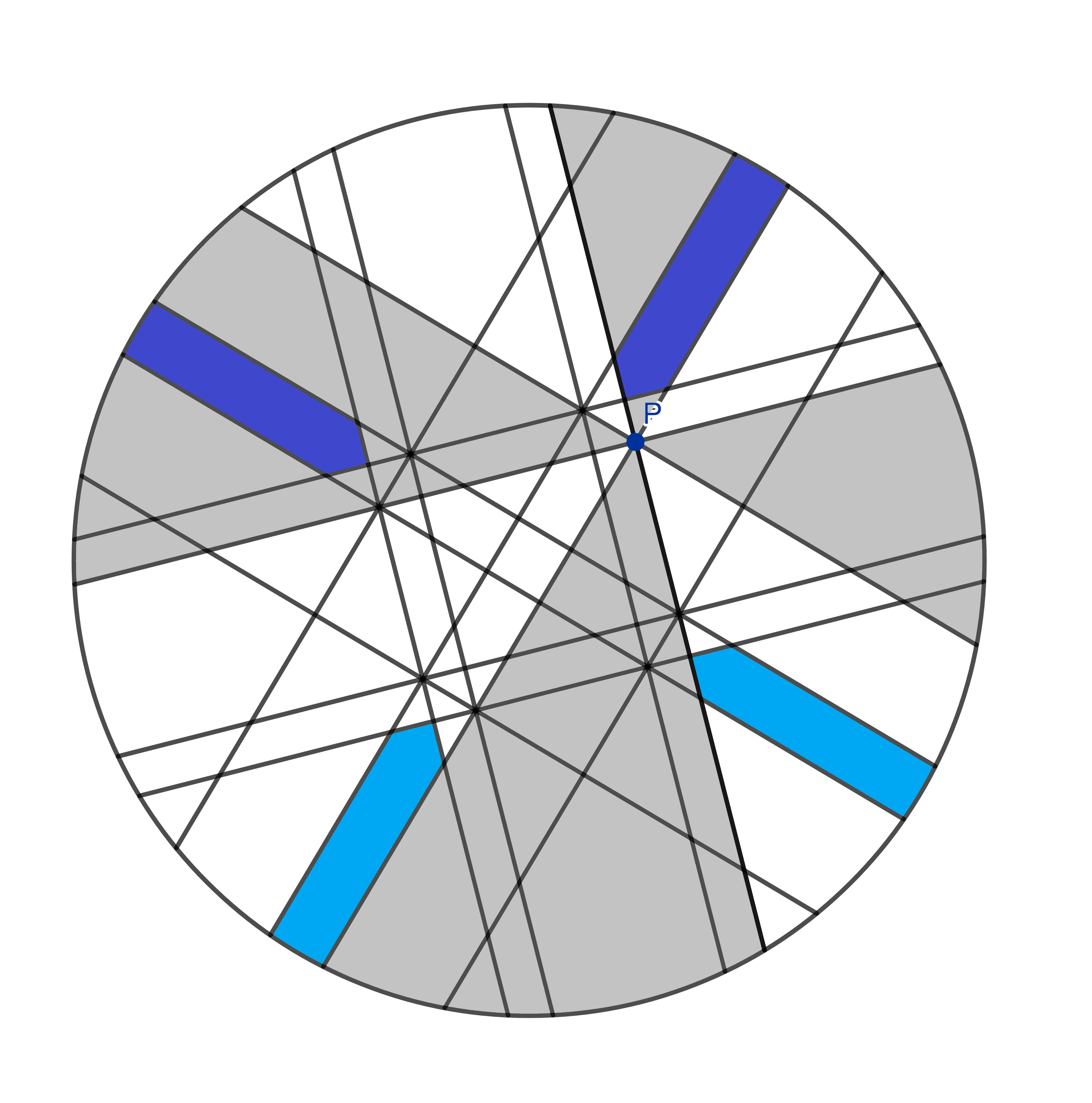
Perfect! We have four of these shapes, all perfect mirror images of each other and therefore, they have the same size. And look, two of these are part of your slices and two are part of mine. So let’s eat those and we’ll both have had the same amount of pizza so far.

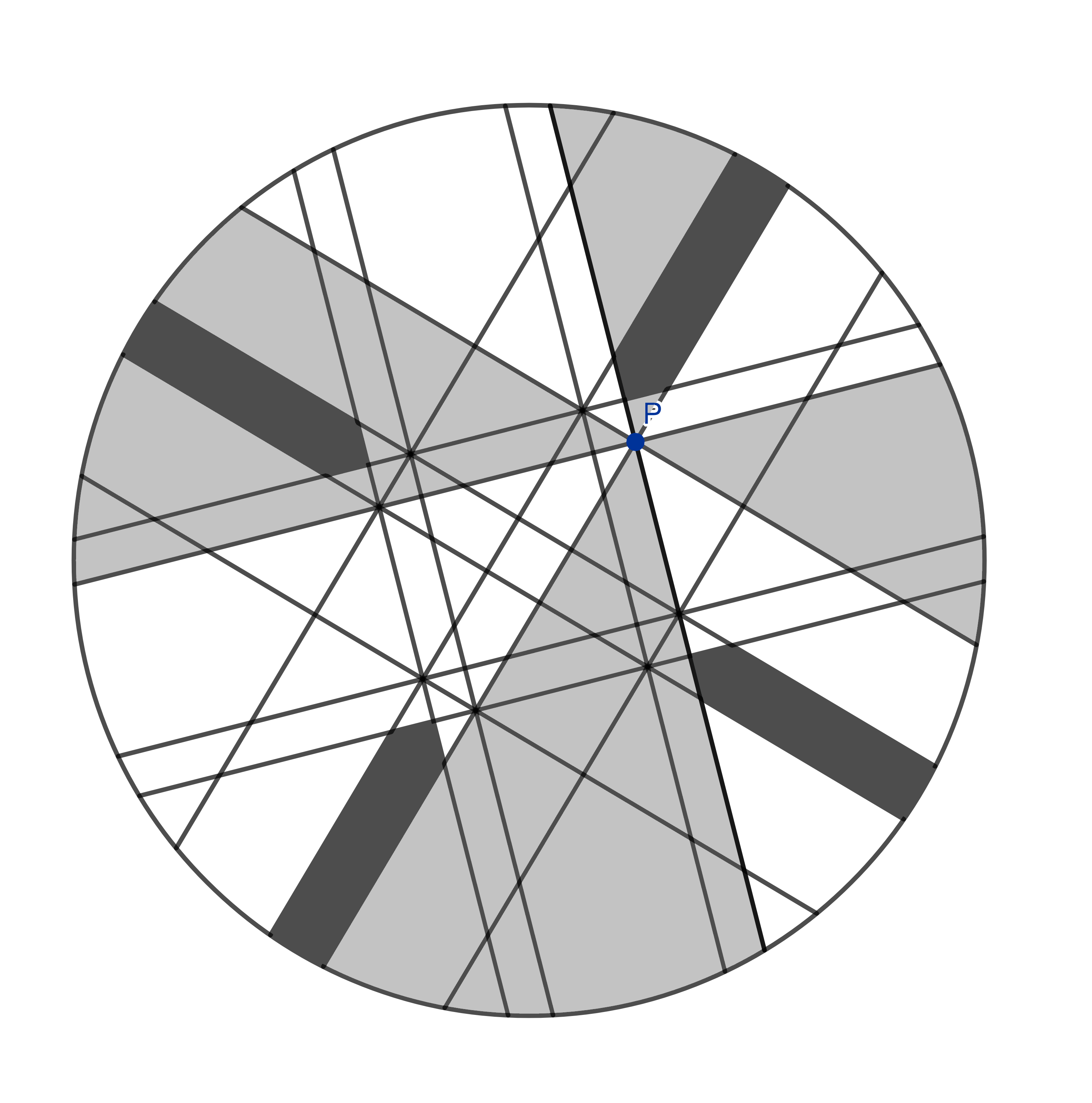
Let’s see what’s next.

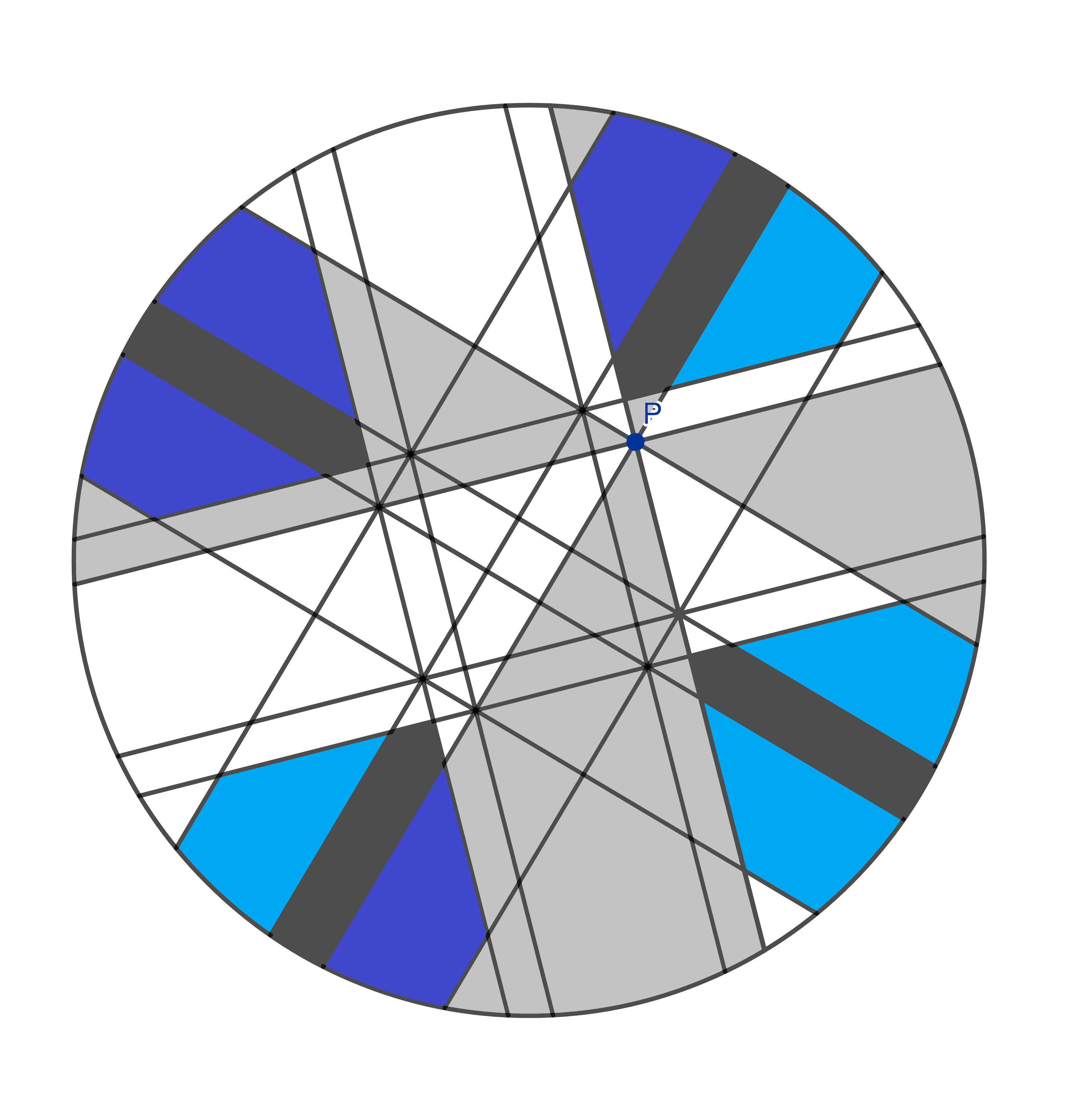
There are these thicker slices, one on each side of the four shapes we just ate. So we have eight in total and again, four of them are yours and four are mine. Bon appetit!

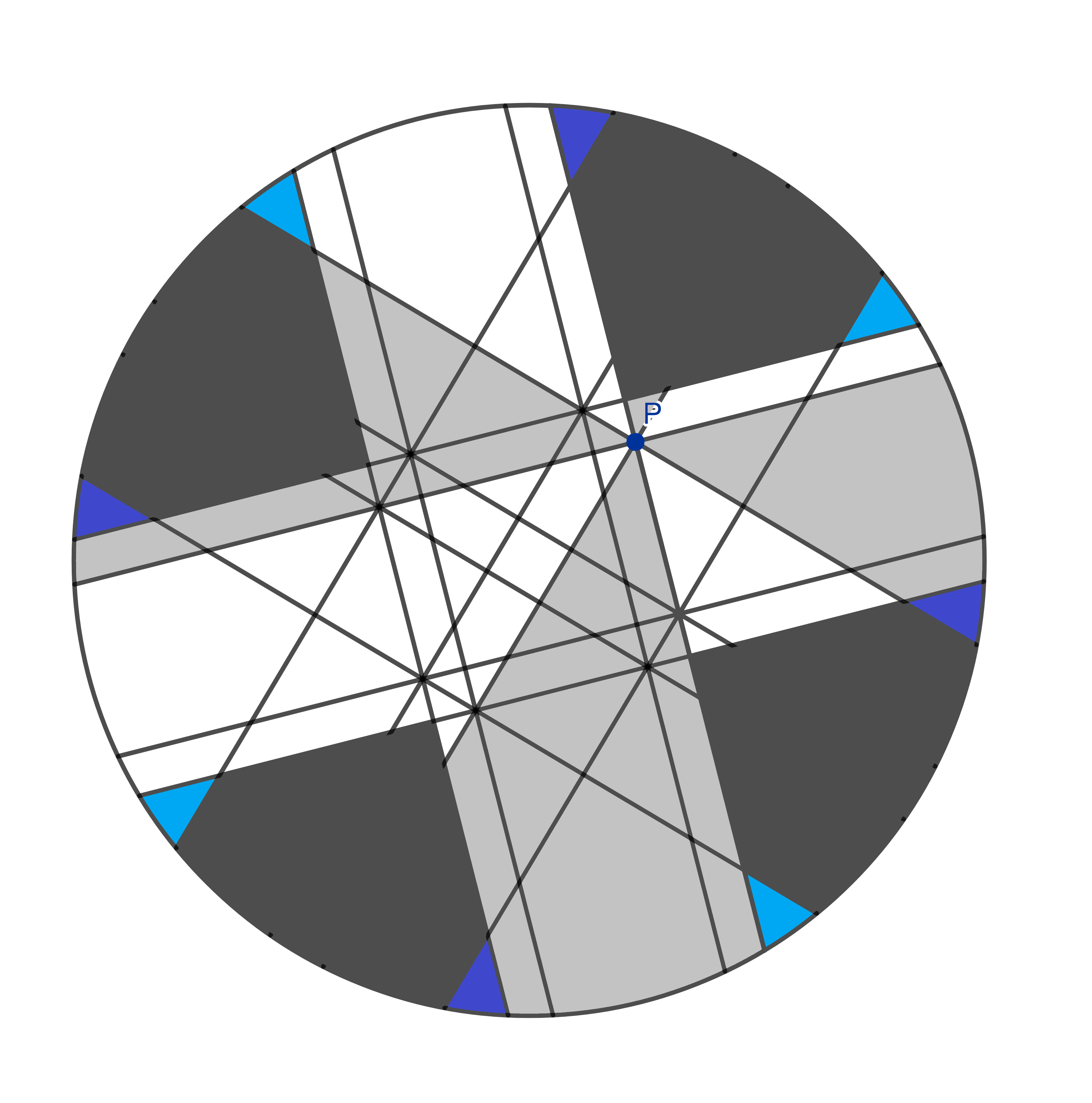
Next to the thicker slices, we have the bits that look like triangles. Again, there are eight of them, four belong to me and four are yours. Dinner time!

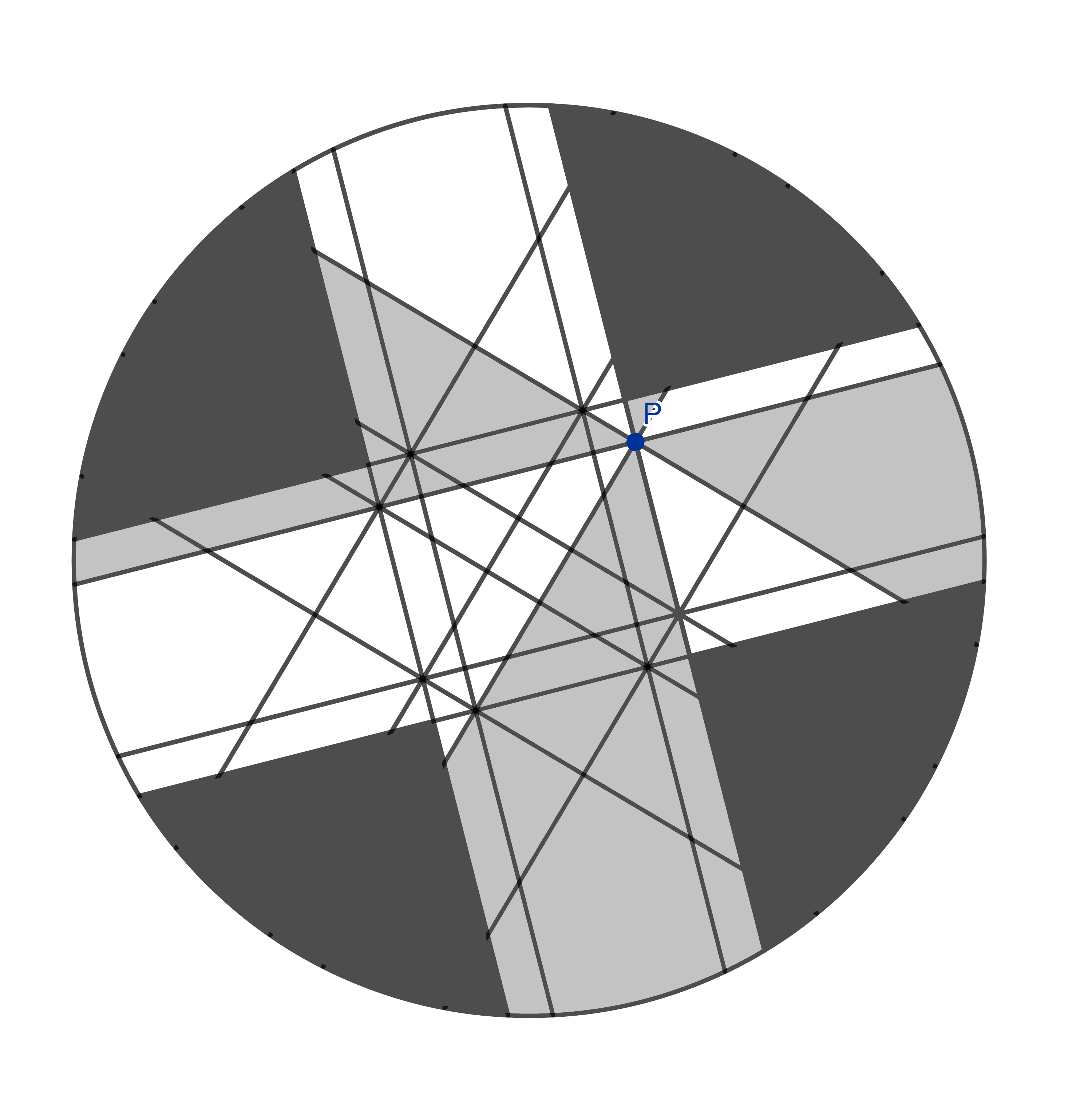
We continue this way, always finding congruent shapes. There are eight of these shapes…

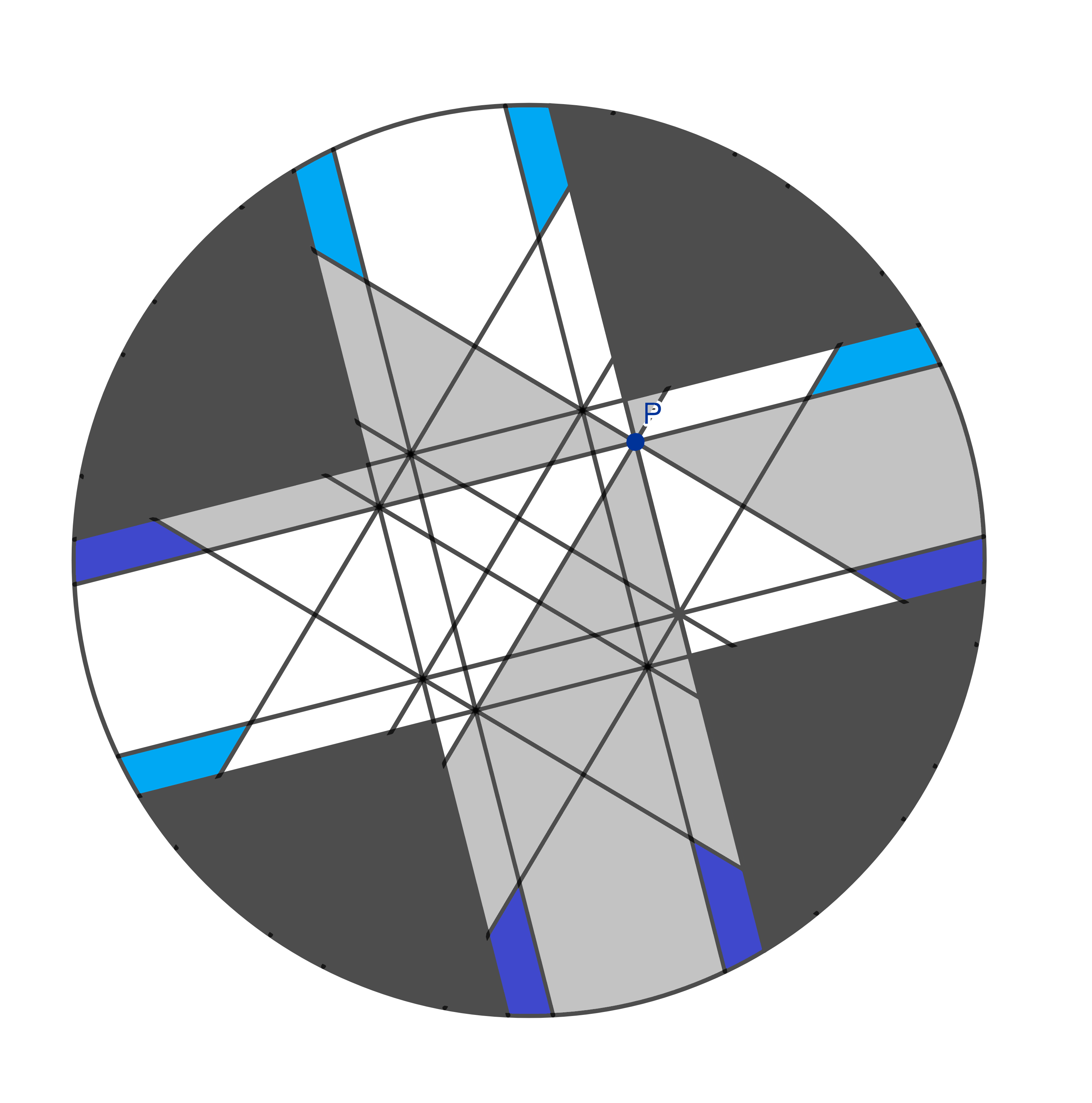
…eight of these…

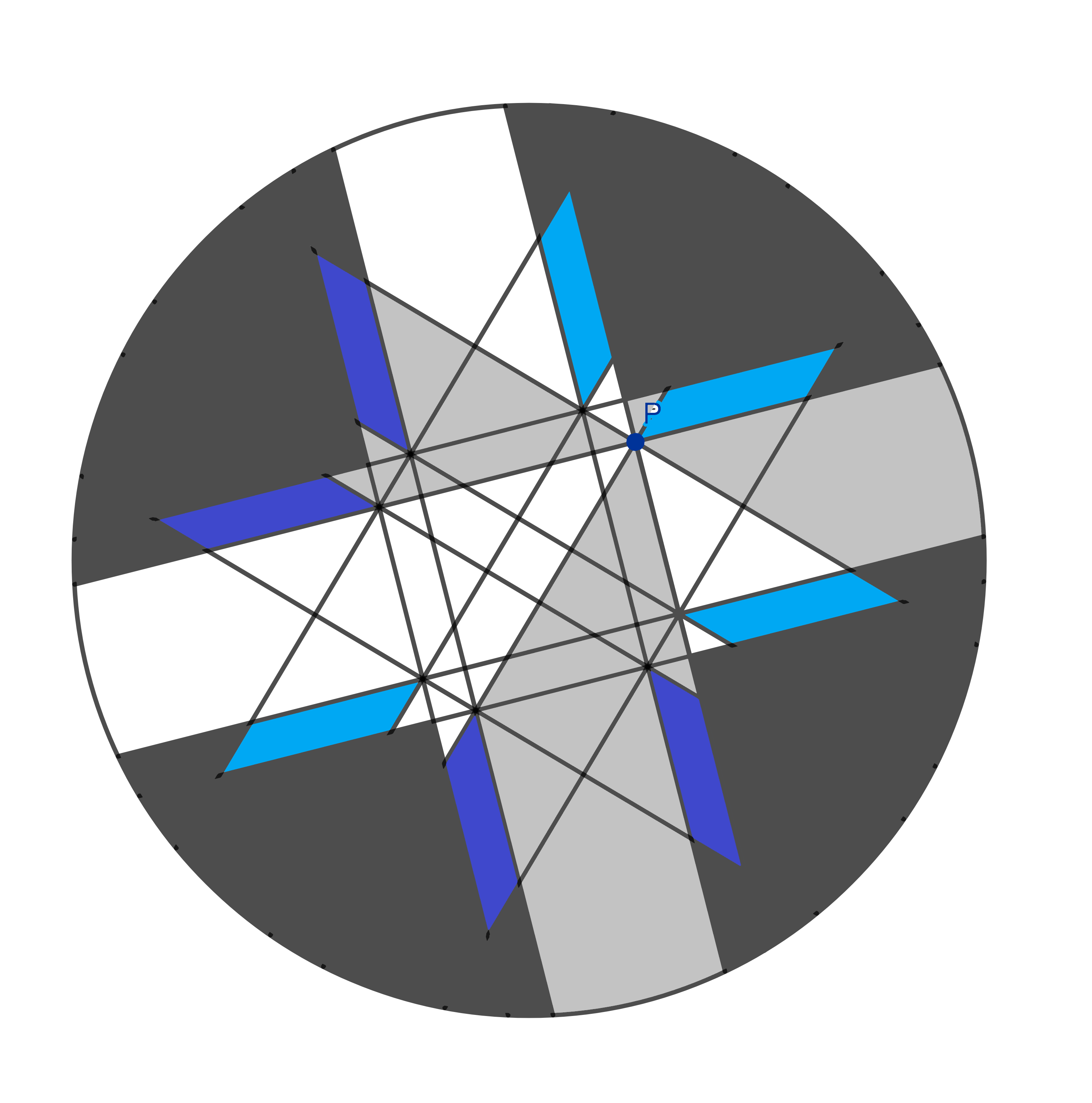
…and another four of these ones.

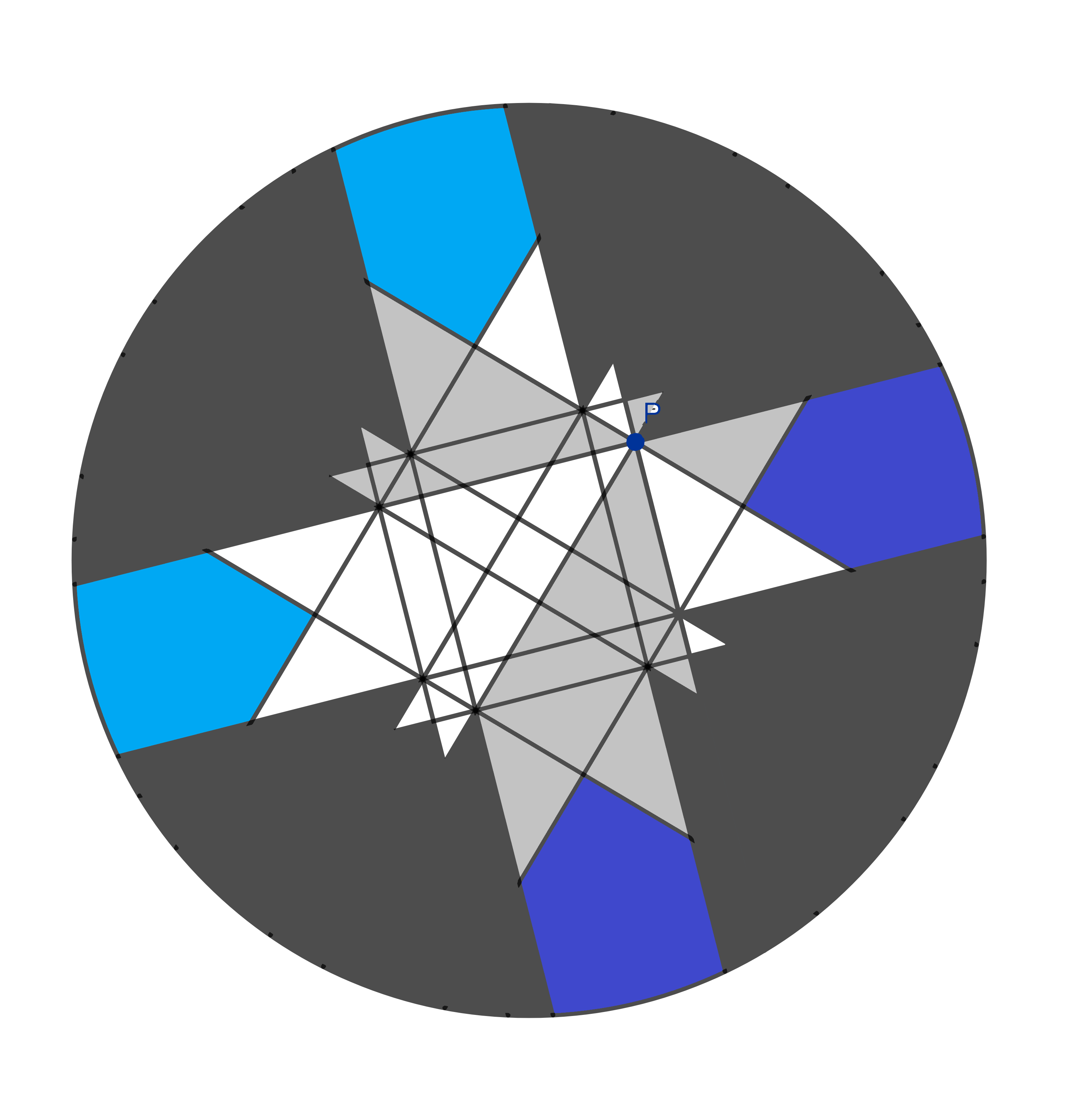
Now we are almost done! There are 12 of the bigger triangles, six for both of us…

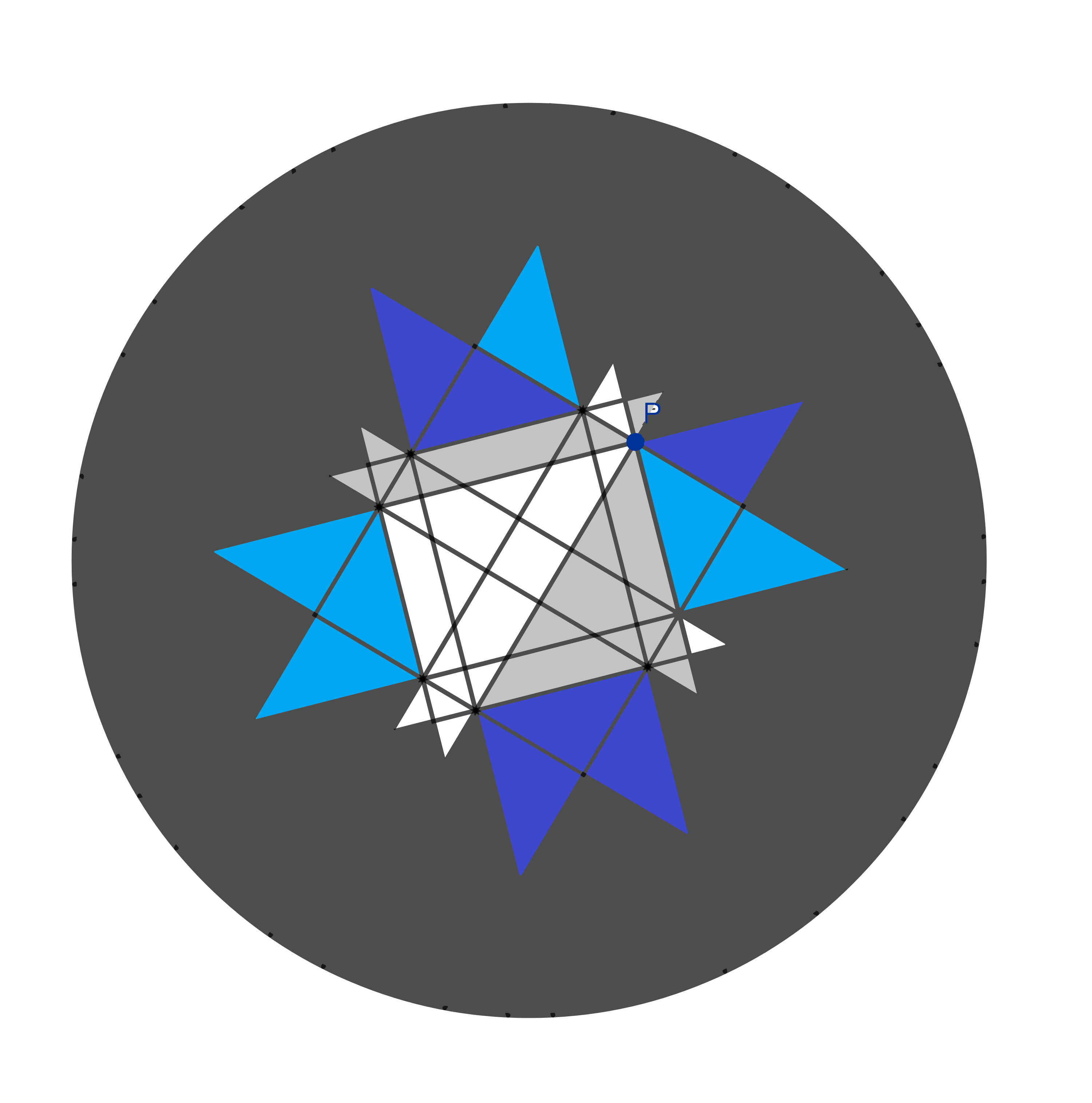
…and 12 smaller triangles.

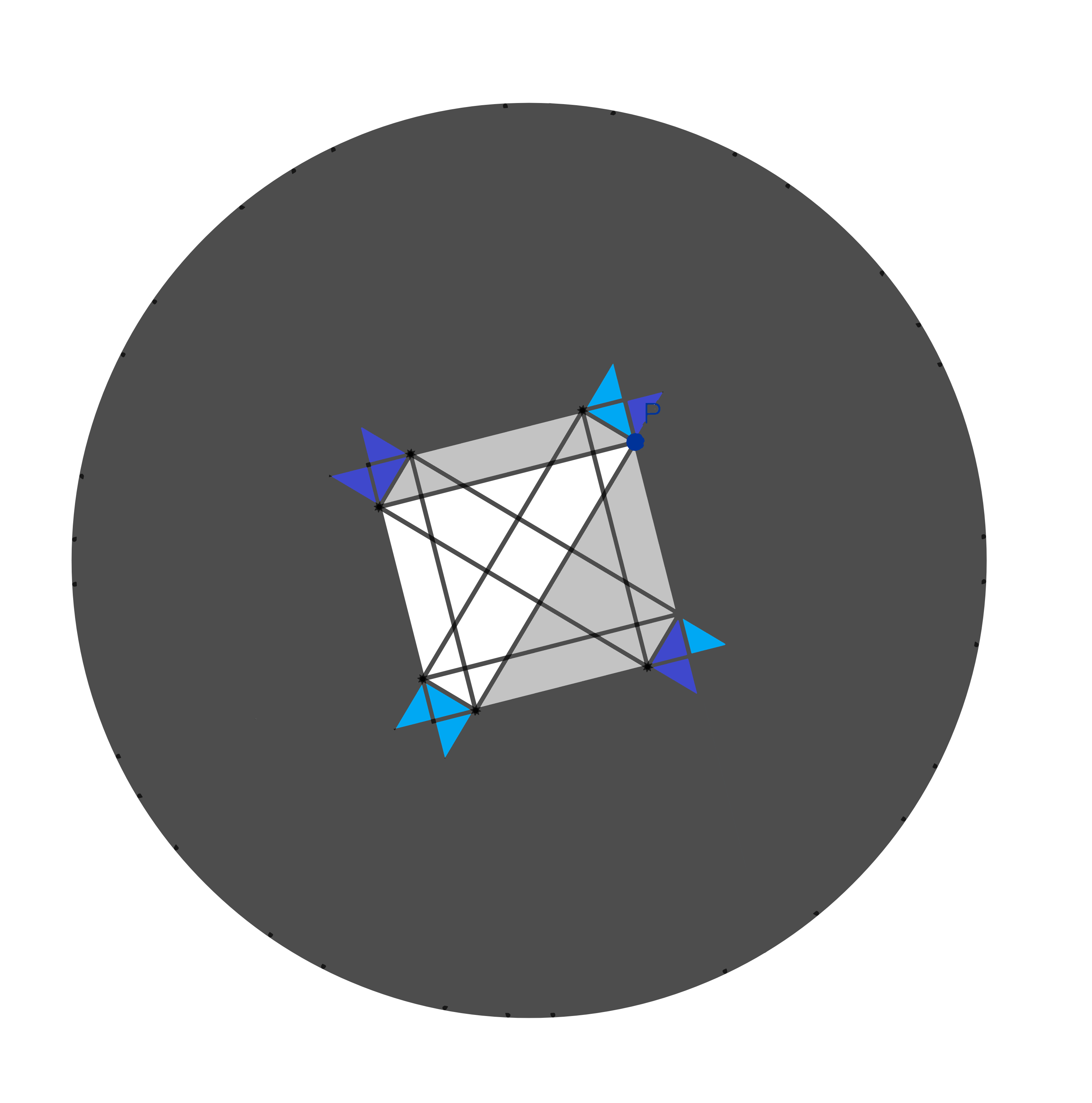
For the remaining bit, I will make one extra cut in red.

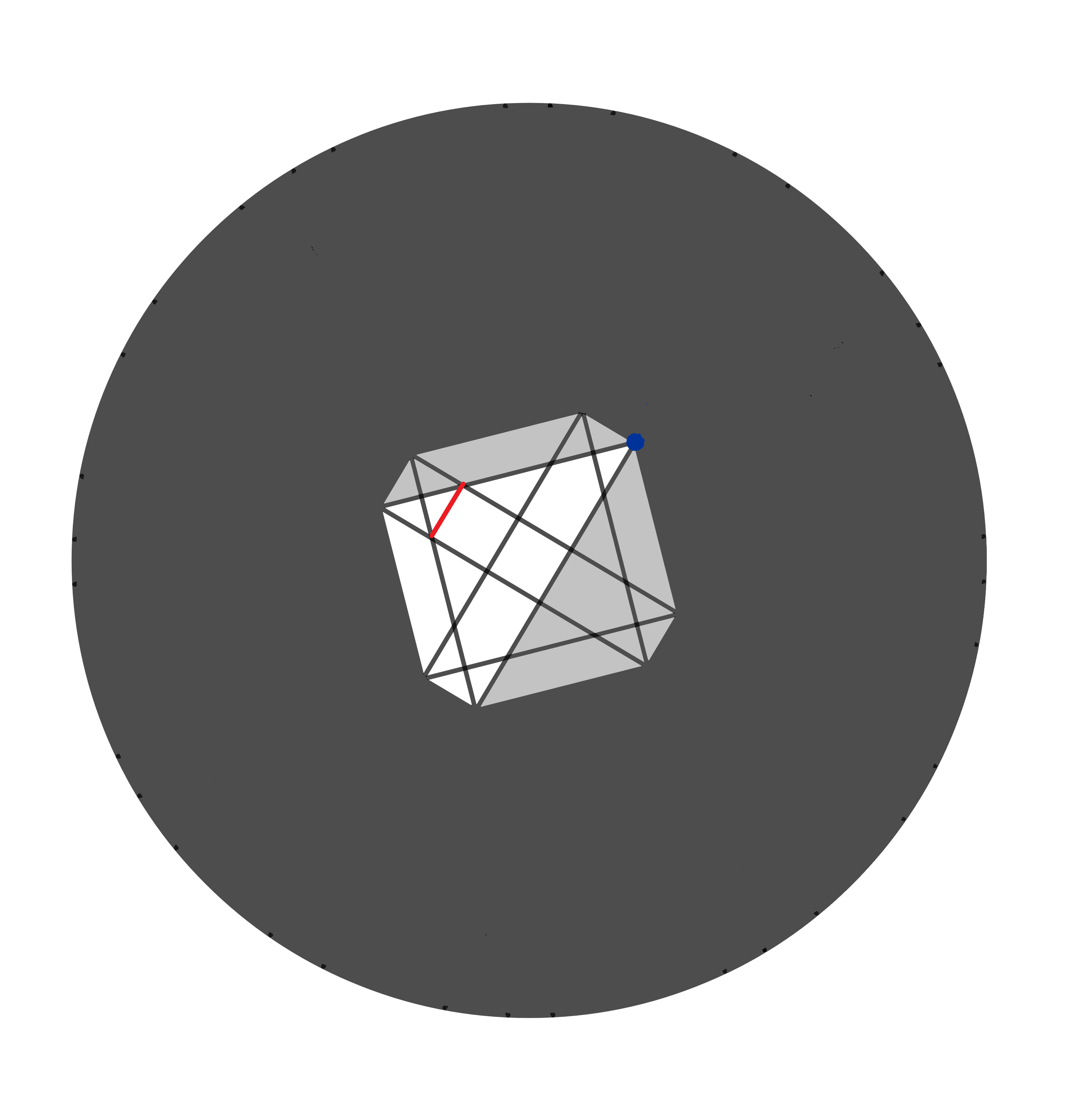
Then, both of us get one large trapezoid…

…three small triangles…

…and finally one thinner trapezoid.

And that’s it. We ate the entire pizza and in every step, we both got the same slices!

Try it yourself

Grab and move the cutting point around in the circle and see if you can find the congruent slices.