Der Satz des Pythagoras

Pythagoras von Samos (570-495 v. Chr.) war ein einflussreicher griechischer Philosoph der Antike, dessen Arbeit verschiedenste Felder von Musik und Philosophie bis hin zu Astronomie und Mathematik revolutionierte - auch wenn du ihn vermutlich nur vom berühmten Satz des Pythagoras kennst.

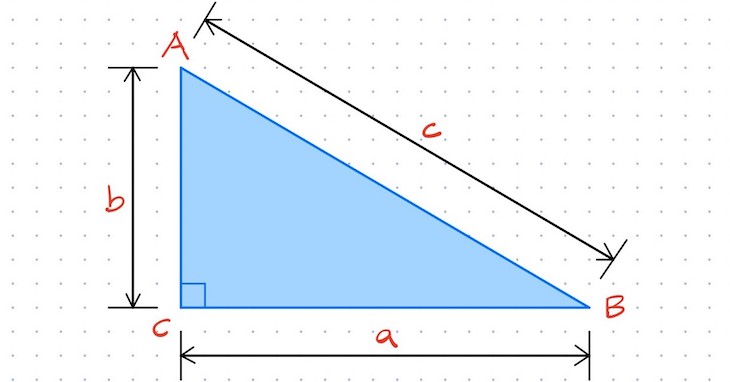
Der Satz des Pythagoras ist ein bekanntes und wegweisendes geometrisches Theorem. Es besagt, dass in einem rechtwinkligen Dreieck (ein Dreieck mit einem 90°-Winkel) das Quadrat der Hypotenuse (die Seite gegenüber von dem 90°-Winkel) genauso groß ist wie die Fläche der beiden Quadrate über den kürzeren Seiten zusammengenommen.

Dieser Satz hat zahlreiche Anwendungen unter anderem in Ingenieurswissenschaften, Gesichtserkennung in Überwachungskameras, Navigationssystemen, etc…

Dann schauen wir mal, ob wir den Satz beweisen können!

Zu zeigen: In einem Dreieck mit einem rechten Winkel (90°-Winkel) hat das Quadrat über der längeren Seite die selbe Fläche wie die beiden Quadrate über der kürzeren Seite zusammen!

Visualisieren wir ein Beispiel

Wir malen ein rechtwinkliges Dreieck und errichten an seinen Seiten Quadrate:

• Ein $3\times 3$-Quadrat an der vertikalen Seite
• Ein $4\times 4$-Quadrat an der horizontalen Seite
• Ein $5\times 5$-Quadrat an der Hypotenuse

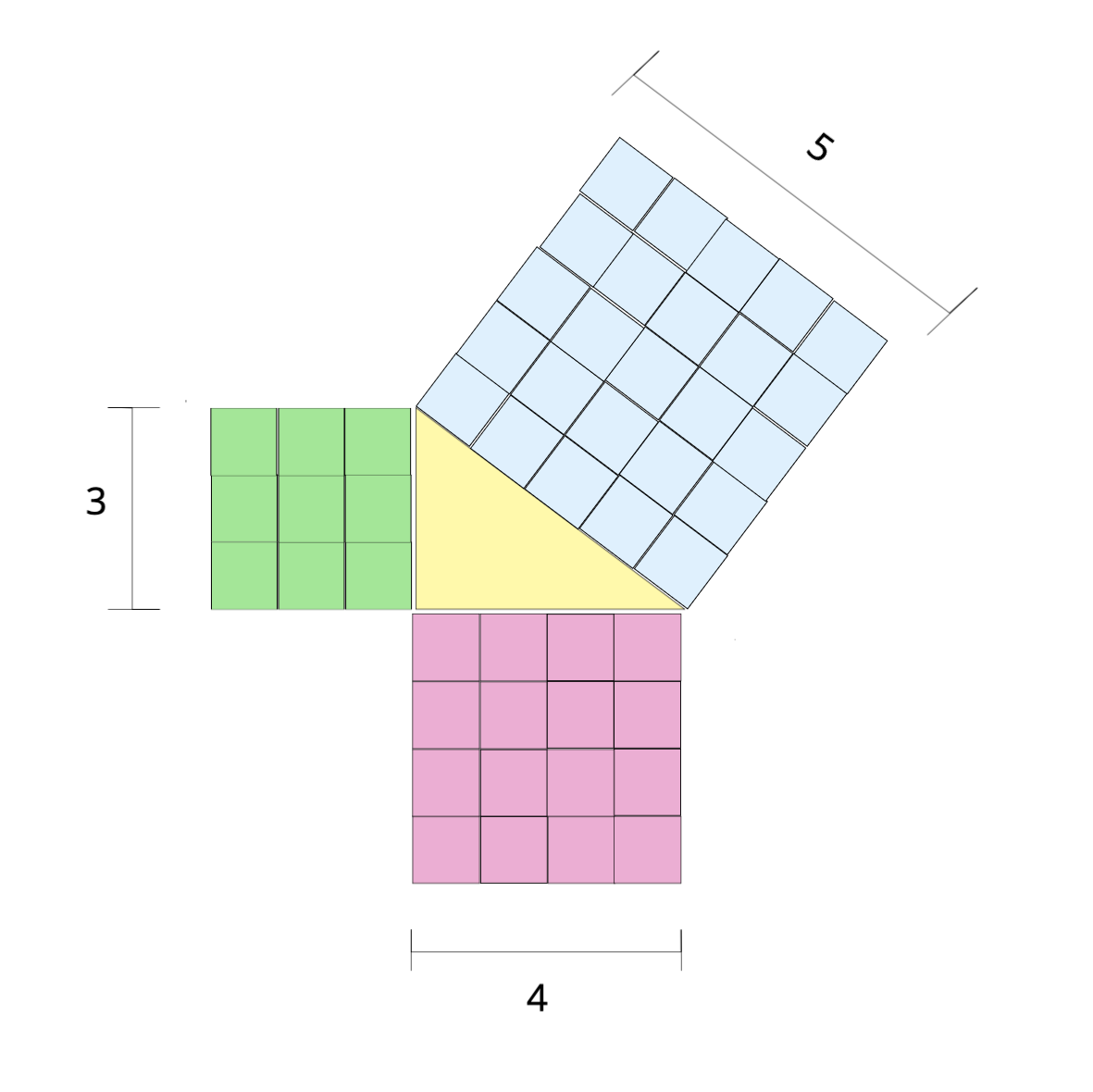
Nach dem Satz sollten die kleineren Quadrate zusammen exakt genauso groß sein wie das Quadrat über der Hypotenuse.

Ist das in unserem Beispiel der Fall?

Schauen wir es uns an! Zähle die Anzahl der kleinen Quadrate und überprüfe, ob in den beiden kleineren Quadrate zusammen genauso viele sind wie im größeren. Wenn du richtig gezählt hast, solltest du 9+16=25 herausbekommen.

Versuch es selbst

Spiele mit den Werten für $a$ und $b$ herum und schau dir an, warum der Satz gilt:

Die Mathematik dahinter

Die Gleichung im Satz des Pythagoras lautet

wobei $a$ und $b$ für die Länge der Katheten steht, die am rechten Winkel anliegen, und $c$ für die Länge der Hypotenuse, die dem rechten Winkel gegenüber liegt.