Pythagorean Theorem

Pythagoras of Samos (570-495 BC) was a very influential ancient greek philosopher, whose work contributed to many fields such as music, philosophy, astronomy and mathematics, the latter including the famous Pythagorean theorem.

The Pythagorean Theorem is a fundamental and certainly well-known geometric theorem. According to this theorem, inh a right-angled triangle (with one of the angles being 90°) the hypotenuse (the longest side, which lies opposite of the 90° angle) is equal to the square root of the sum of the areas of the squares on the other two sides.

This theorem has a wide-set of applications including engineering and construction fields, face recognition in security cameras, navigation and many more.

To be proven: When a triangle has a right angle (90°) and squares are made on each of the three sides, then the biggest square has the exact same area as the other two squares put together!

Let’s visualize the statement above

We draw a right-angled triangle and next to the sides of the triangle, we draw squares:

• A $3\times 3$ square for the height (side)
• A $4\times 4$ square for the width (side)
• A $5\times 5$ square for the hypotenuse

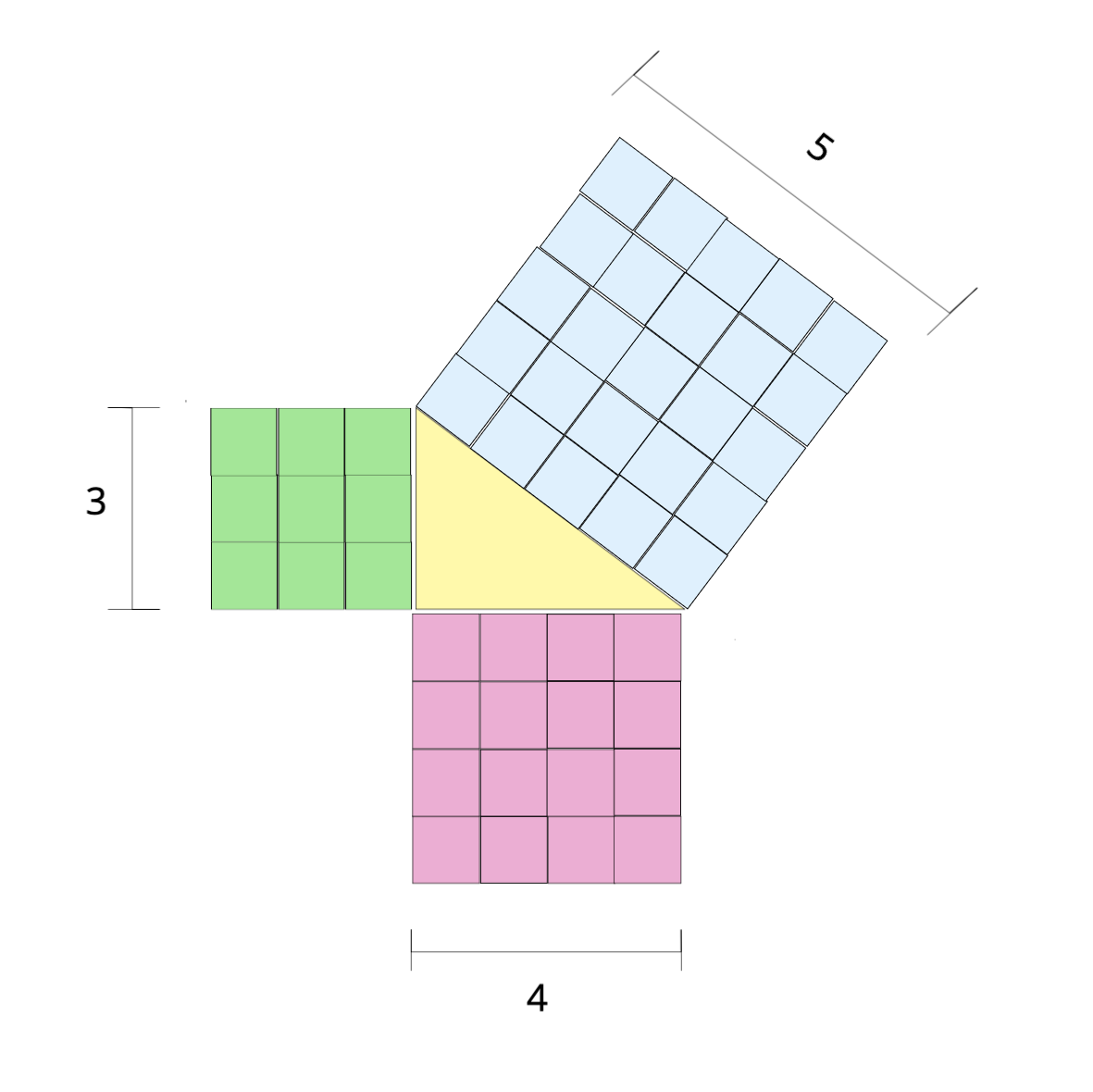
According to the theorem the sum of the squares of the shorter sides should equal the square of the hypotenuse.

Is that the case in our visualization?

Let’s check it out: Count the small squares of the sides, sum them up and compare if the sum of the sides equals the amount of squares of the hypotenuse. You should be getting 9 + 16 = 25.

Try it yourself

Play around with $a$ and $b$ to see that this theorem holds. See how the forms slide into eachother, which shows why these areas are of equal size.

The math behind it

The equation to express the theorem in a right-angled triangle is

where $a$ and $b$ represent the cathetuses, otherwise known as the legs adjacent or opposite-sided of the right angle and $c$ is the hypotenuse.