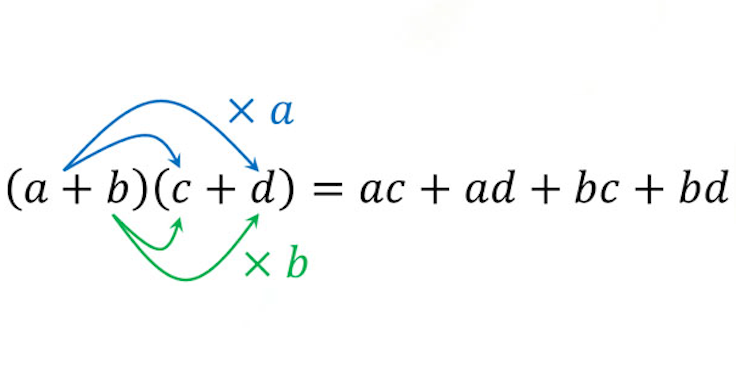
Expansion polynomiale

Un polynôme est défini comme une expression composée de variables, de constantes et d’exposants, qui sont fusionnés à l’aide d’opérations mathématiques telles que l’addition, la soustraction, la multiplication et la division par des nombres. D’autre part, une expansion d’un produit de sommes en mathématiques l’exprime comme une somme de produits en raison des propriétés distributives de la multiplication par rapport à l’addition.

Après avoir défini ces deux termes, nous pouvons maintenant répondre à la question suivante:

Qu’est-ce qu’un développement polynomial?

Le développement d’un polynôme est une expression du même polynôme, où aucune variable n’apparaît entre parenthèses et où tous les termes identiques ont été combinés.

Comment développer un polynôme?

Si nous avons une ou deux expressions à multiplier, nous pouvons facilement le faire manuellement. Mais qu’en est-il si nous avons une expression de la forme : $(3a+2{)}^4$. Multiplier le tout 4 fois à la main prend du temps. </p> <p>Par chance, il existe quelques modèles que nous pouvons utiliser.</p> <p>

Expansion avec le triangle de Pascal

Le triangle de Pascal a été nommé d’après le célèbre et révolutionnaire mathématicien français du XVIIe siècle Blaise Pascal (1623-1662 AD). Il s’agit d’une représentation visuelle triangulaire des coefficients binomiaux, qui sont essentiels pour développer les polynômes. Ce modèle était connu et pratiqué en Extrême-Orient et au Proche-Orient des siècles avant le monde occidental.

Comment construire un tel triangle

• Le triangle commence par un 1 au sommet et, en dessous, par un 1 à gauche et à droite.
• Pour les rangées suivantes, chaque nombre est la somme des deux nombres qui le précèdent dans la rangée précédente.

Comment développer à l’aide du triangle?

Étant donné $(a+b{)}^n$ pour toute puissance $n$, vous pouvez écrire le développement en utilisant les coefficients du triangle. Notez que pour écrire les coefficients pour toute puissance $n$, vous devez regarder la ligne $n+1$ pour trouver les coefficients.

Ainsi, pour l’exemple ci-dessus $(3a+2{)}^4$, il faudrait vérifier la 5ème ligne du triangle de Pascal pour trouver les coefficients, qui sont 1, 4, 6, 4, 1. En connaissant les coefficients, nous pouvons transformer le polynôme de la classe de 4e en:

Il suffit alors de multiplier:

Développement des polynômes du 2e degré avec plus de deux variables

Dans les exemples précédents, nous avons vu comment développer des binômes, mais que se passe-t-il si nous avons plus de deux variables? Dans ce cas, comment procéder?

Dans ce qui suit, nous allons essayer de prouver visuellement comment les polynômes du 2e degré peuvent être développés.

Jouons au détective ! Pouvez-vous repérer un motif?

Alerte spoiler: Consultez le post sur La somme de $n$ entiers impairs et voir ce que nous avons utilisé pour représenter les nombres carrés.

Comme vous l’avez peut-être deviné, nous avons utilisé un carré. Par exemple, si nous voulons calculer la somme de deux variables $(a+b{)}^2$ le résultat est le même que celui que l’on obtiendrait en calculant la surface d’un carré de hauteur et de largeur $a+b$.

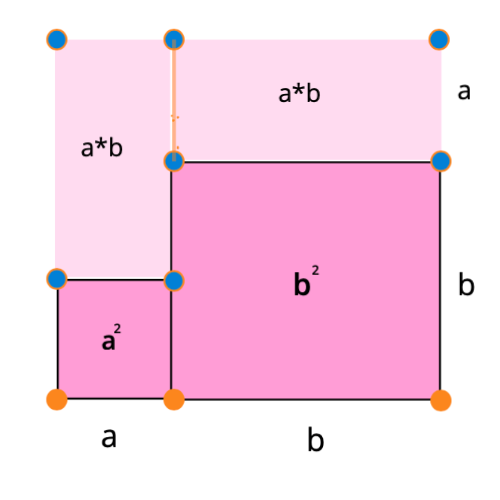
et en construisant un carré tel que celui présenté dans l’image ci-dessus, on peut visiblement voir que la surface est la somme de $a^2$, $b^2$ and $2ab$, qui prouve l’identité algébrique:

Essayez vous-même

Utilisez le curseur ci-dessous pour développer le carré pour différents nombres de variables.