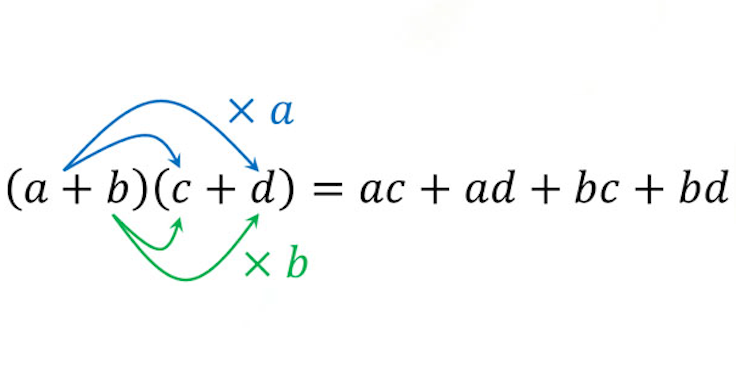
Polynomielle Erweiterung

Ein Polynom ist ein mathematischer Ausdruck, der aus Variablen, Konstanten und Exponenten besteht, welche durch mathematische Operationen wie Addieren, Subtrahieren, Multiplizieren oder Dividieren durch Konstanten zusammengefügt wurden. Eine Erweiterung eines Produkts von Summen nutzt das sogenannte Distributivgesetz der Multiplikation und Addition um das Produkt von Summen anders darzustellen. Wir sagen dazu auch ausmultiplizieren.

Nachdem wir diese beiden Begriffe eingeführt haben, können wir die folgende Frage beantworten:

Was ist eine polynomielle Erweiterung?

Die Erweiterung eines Polynoms ist die Erweiterung eines Polynoms, in der keine der Variablen in Klammern vorkommt und alle Summanden miteinander kombiniert wurden.

Wie erweitert man ein Polynom?

Falls wir einen oder zwei Ausdrücke haben, die wie ausmultiplizieren sollen, können wir das einfach per Hand machen. Aber was, wenn wir eine komplexere Formel haben wie zum Beispiel: $(3a+2{)}^4$. Diesen gesamten Ausdruck viermal per Hand auszumultiplizieren dauert sehr lange.

Glücklicherweise gibt es dabei einige Muster, die wir uns zu Nutze machen können.

Erweiterung mithilfe des Pascalschen Dreiecks

Das Pascalsche Dreieck hat seinen Namen dank des berühmten und revolutionären französischen Mathematiker Blaise Pascal (1623-1662 n. Chr.). Hier werden in Form eines Dreiecks sogenannte Binomialkoeffizienten dargestellt, die essentiell für das Ausmultiplizieren von Polynomen sind. Dieses Muster war der östlichen Welt schon lang bekannt, bevor es im Westen entdeckt wurde.

Wie konstruiert man dieses Dreieck?

• Das Dreieck startet mit einer 1 an der Spitze und darunter je eine 1 auf der linken und rechten Seite
• In den folgenden Reihen ergibt sich jede weitere Zahl als die Summe der beiden Zahlen schräg links und schräg rechts über ihr.

Wie kann man diesen Dreieck für polynomielle Erweiterung benutzen?

Für einen beliebigen Exponennten $n$ können wir den Ausdruck $(a+b{)}^n$ mithilfe der Koeffizienten im Dreieck umschreiben. Um die richtigen Koeffizienten für den Ausdruck $n$ zu erhalten, müssen wir uns die $n+1$-te Reihe ansehen.

Demnach müssen wir uns für das Beispiel von oben $(3a+2{)}^4$, die fünfte Reihe des Pascalschen Dreiecks anschauen, wo wir die folgenden Koeffizienten finden: 1, 4, 6, 4, 1. Mithilfe dieser Koeffizienten können wir dieses Polynom von viertem Grad umschreiben als:

Jetzt müssen wir nur noch ein wenig ausmultiplizieren:

Erweiterung von Polynomen zweiten Grades mit mehr als zwei Variablen

In den vorherigen Beispielen haben wir gesehen, wie wir Binome erweitern können. Aber was, wenn wir mehr als zwei Variablen haben?

Jetzt zeigen und beweisen wir euch, wie man Polynome vom zweiten Grad erweitern kann.

Kannst du das Muster erkennen?

Spoiler: Schau dir den Beitrag zu der Summe von $n$ ungeraden Zahlen an und sieht, wie wir dort Quadratzahlen darstellen.

Wie du dir bestimmt gedacht hast, nutzen wir dafür ein Quadrat. Demnach ist das Quadrat der Summe zweier Variablen $(a+b{)}^2$ nichts anderes als die Fläche eines Quadrats mit Höhe und Breite $a+b$

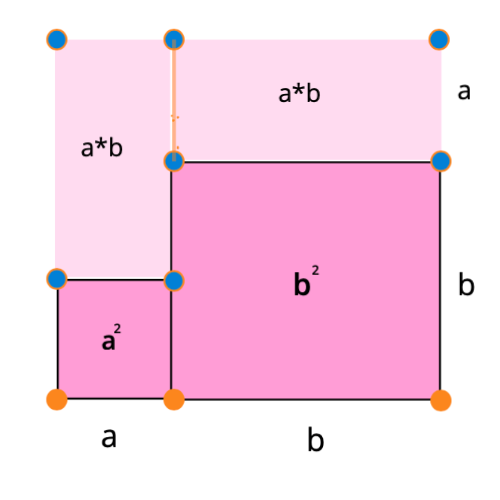
Durch die Konstruktion eines solchen Quadrats können wir sehen, in welche kleineren Flächen sich das größere Quadrat aufteilen lässt: $a^2$, $b^2$ and $2ab$ Das beweist die folgende algebraische Identität:

Versuch es selbst

Benutze den Schieber, um verschiedene Anzahlen von Variablen auszuprobieren.