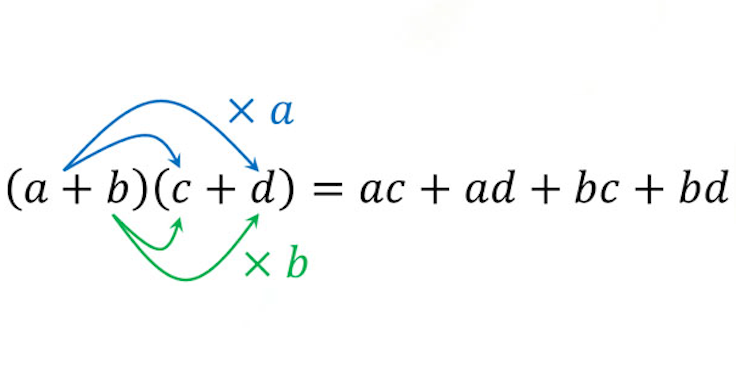
Polynomial expansion

A polynomial is defined as an expression which is made of variables, constants and exponents, that are merged using mathematical operations such as addition, subtraction, multiplication and division by numbers. On the other hand, an expansion of a product of sums in mathematics expresses it as a sum of products as a result of distributive properties of multiplication over addition.

So now after we defined these two terms we can answer the question:

What is a Polynomial Expansion?

The expansion of a polynomial is an expression of the same polynomial, where no variable appears within parentheses and all identical terms have been combined.

How to expand a Polynomial?

If we have one or two expressions to be multiplied, we can easily do it manually. But what if we have an expression of the form: $(3a+2{)}^4$. Multiplying the whole thing 4 times by hand sure does take some time.

To our luck, there are some patterns we can use.

Expansion with Pascal’s Triangle

Pascal’s triangle was named after the famous and revolutionary french mathematician of the 17th century Blaise Pascal (1623-1662 AD) and it is a visual triangular representation of the binomial coefficients, which are essential for expanding polynomials. This pattern was known and practiced in the far and near east centuries before the western world.

How to construct a such triangle

• The triangle starts with a 1 on top and below that a 1 on the left and right side.
• For the following rows below, every number is the sum of the two numbers that are above it in the previous row.

How to expand with the help of the triangle?

Given $(a+b{)}^n$ for any power $n$ you can write out the expansion using the coefficients from the triangle. Note that to write the coefficients for any power $n$, you need to look at row $n+1$ to find the coefficients.

So for the example above $(3a+2{)}^4$, we would have to check the 5th row of Pascal’s triangle to find the coefficients, which are 1, 4, 6, 4, 1. Knowing the coefficients we can transform the polynom of the 4th grade to:

Then it’s only a matter of multiplying:

Expansion of polynomials of the 2nd degree with more than two variables

In the previous examples we saw how one could expand binomials, but what if we have more than two variables. How do we proceed in that case?

In the following we are going to try and visually prove how polynomials of the 2nd degree can be extended.

Let’s play detective! Can you spot a pattern?

Spoiler Alert: Check the post about The sum of $n$ odd integers and see what we used to represent square numbers.

As you may have guessed it, we used a square. So for example if we want to calculate the sum of two variables $(a+b{)}^2$ the result is the same as what we would get when calculating the surface area of a square of height and width $a+b$.

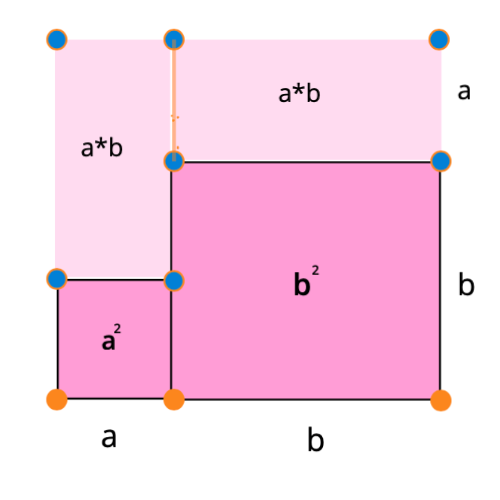
and by constructing such a square such as shown in the picture above, one can visibly see that the surface area is the sum of $a^2$, $b^2$ and $2ab$, which proves the algebraic identity:

Try it yourself

Use the slider below to expand the square for different numbers of variables.