Théorème de la pizza

Hé, j’ai apporté quelque chose pour nous…

J’ai acheté une pizza à partager pour nous deux! Qui peut faire des maths l’estomac vide? Il ne me reste plus qu’à la découper en tranches…

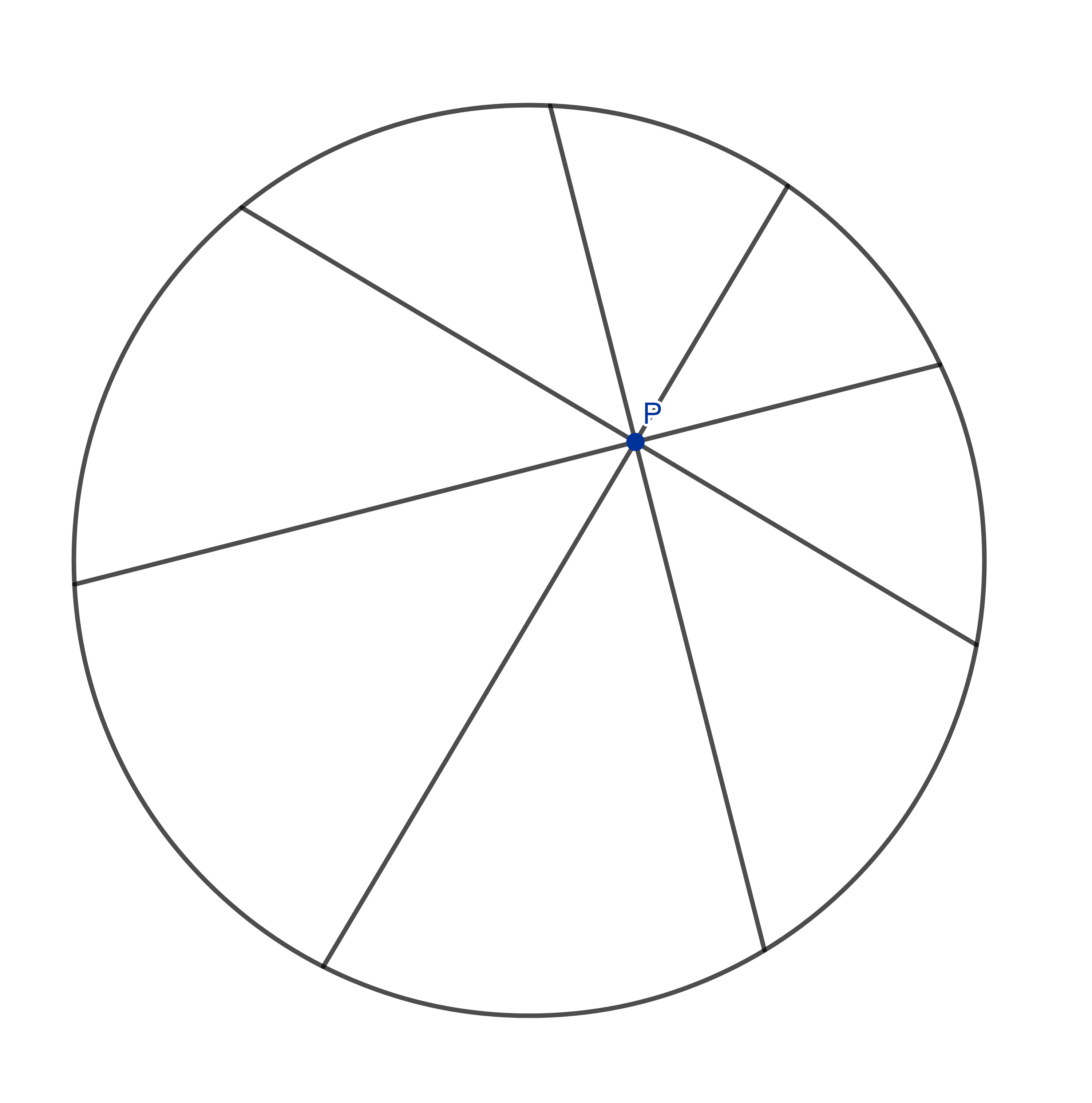
Oups. Ça n’a pas l’air joli du tout! J’ai fait toutes les coupes de manière régulière, de sorte que les huit angles entre les coupes sont également espacés et forment un angle de 45°. Mais je n’ai pas du tout touché le centre de la pizza, ce qui fait que toutes les parts ont l’air vraiment bizarres. Mais ne vous inquiétez pas: si nous faisons le tour du cercle, que vous prenez une part sur deux et que je prends le reste, nous aurons exactement la même quantité de pizza!.

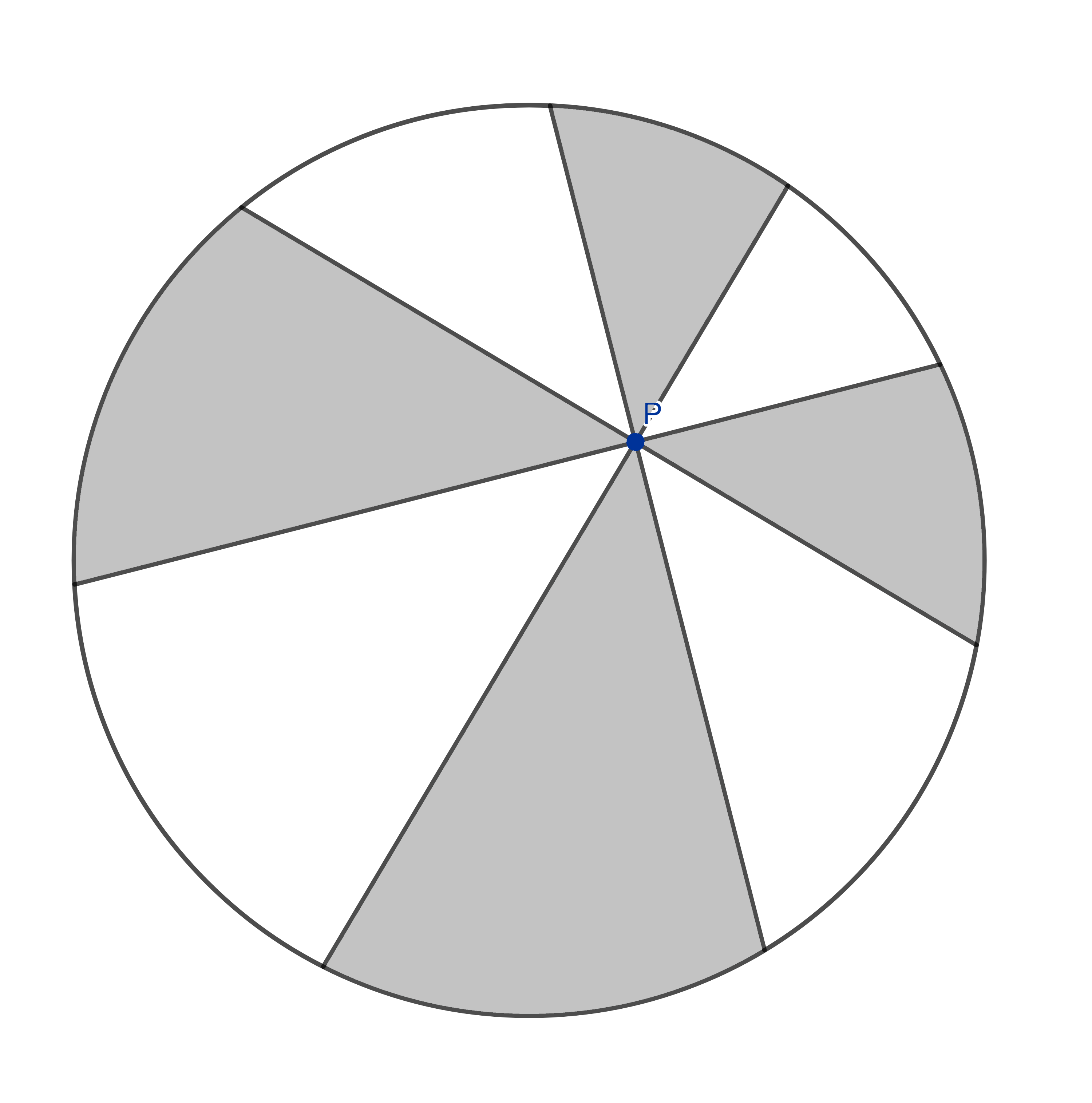
C’est ce qu’on appelle aussi le théorème de la pizza. Qui a dit que les mathématiques n’étaient pas utiles dans le monde réel? Et nous allons même le prouver ensemble!

Prouver le théorème de la pizza

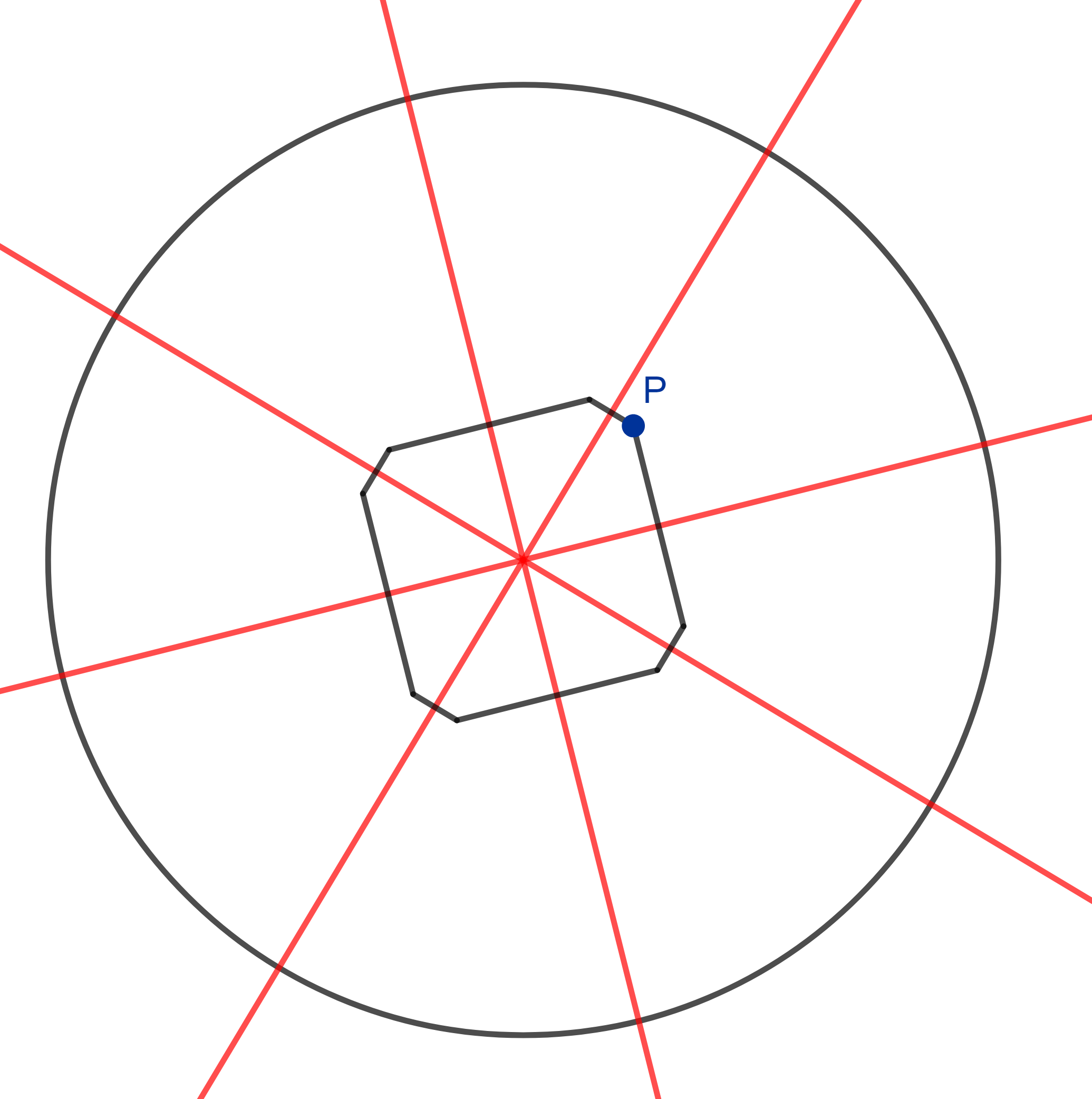
Comment prouver que vos quatre tranches ont la même surface que mes quatre tranches? Après tout, elles ont toutes l’air complètement différentes. Dans ce cas, il peut être utile d’ajouter quelques lignes à votre construction géométrique - ou de découper votre pizza - afin de créer davantage de formes ayant clairement la même surface. Deux formes sont dites congruentes si elles ont exactement la même forme, la même taille et la même surface. Une bonne façon de créer des formes congruentes est d’utiliser des symétries, par exemple en faisant miroiter certaines lignes. C’est exactement ce que nous allons faire! Nous prenons les coupes que nous avons faites et nous les déplaçons vers le centre de la pizza (en rouge). En réfléchissant le point de coupe le long de ces lignes, nous obtenons un octogone (en noir).

Si nous reflétons également les coupes que nous avons effectuées précédemment, nous obtenons la pizza découpée suivante.

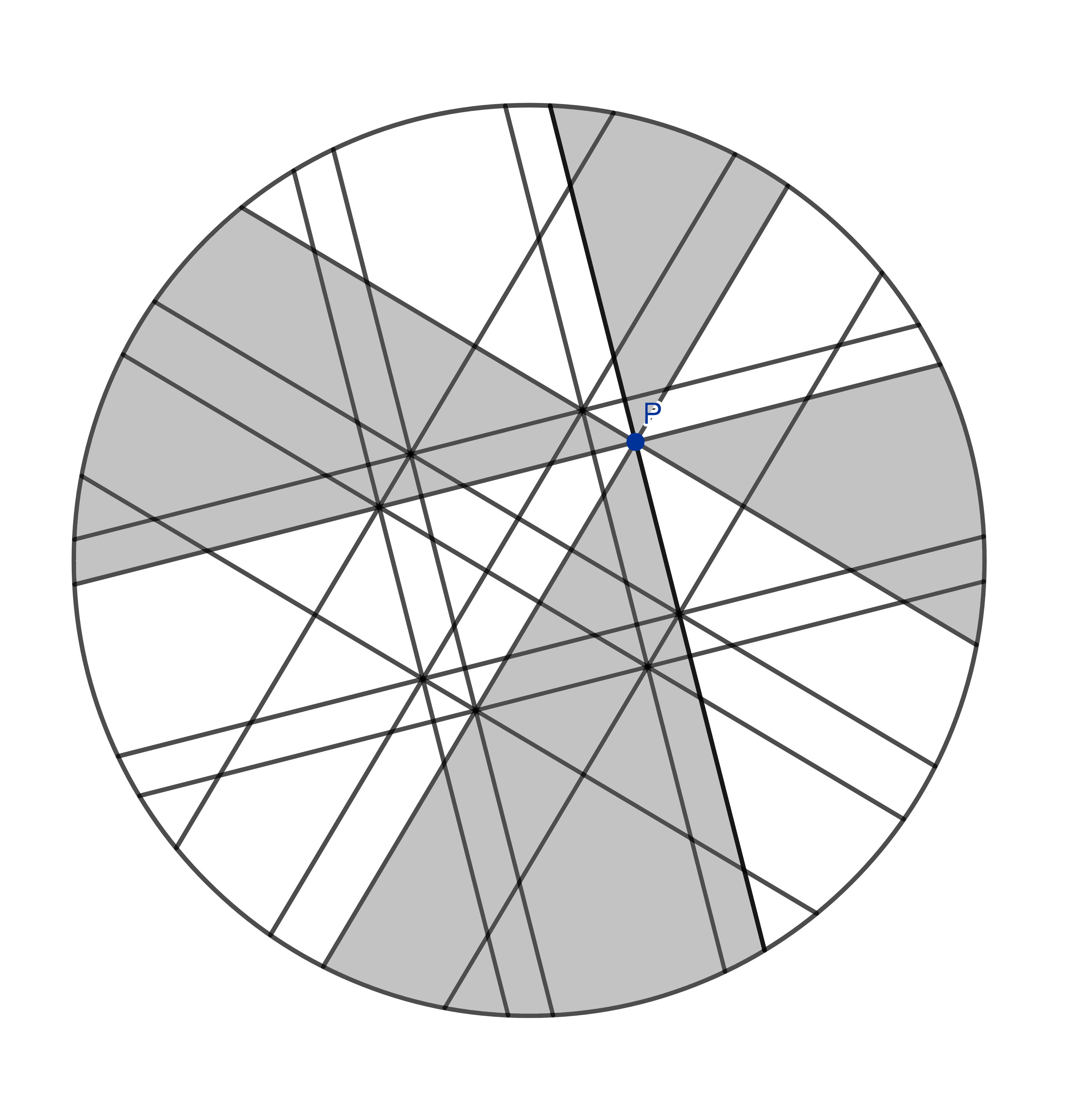
Ne paniquez pas ! Cela semble très compliqué, mais nous allons nous concentrer sur une mini-tranche à chaque fois et trouver toutes les autres mini-tranches qui lui ressemblent exactement. Commençons par celle-ci:

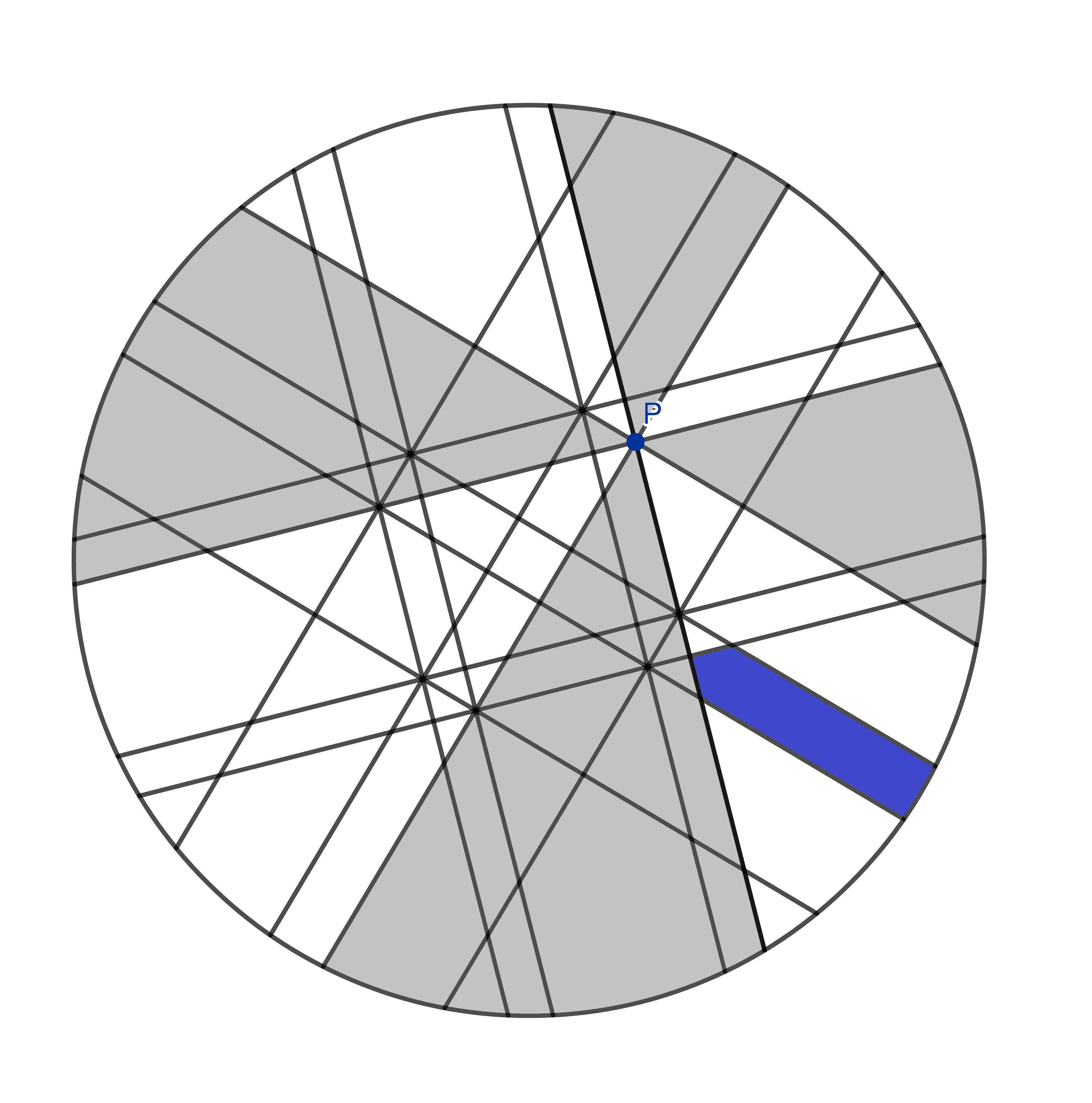
Il y a trois autres parties comme celle-ci. Pouvez-vous les trouver?

.

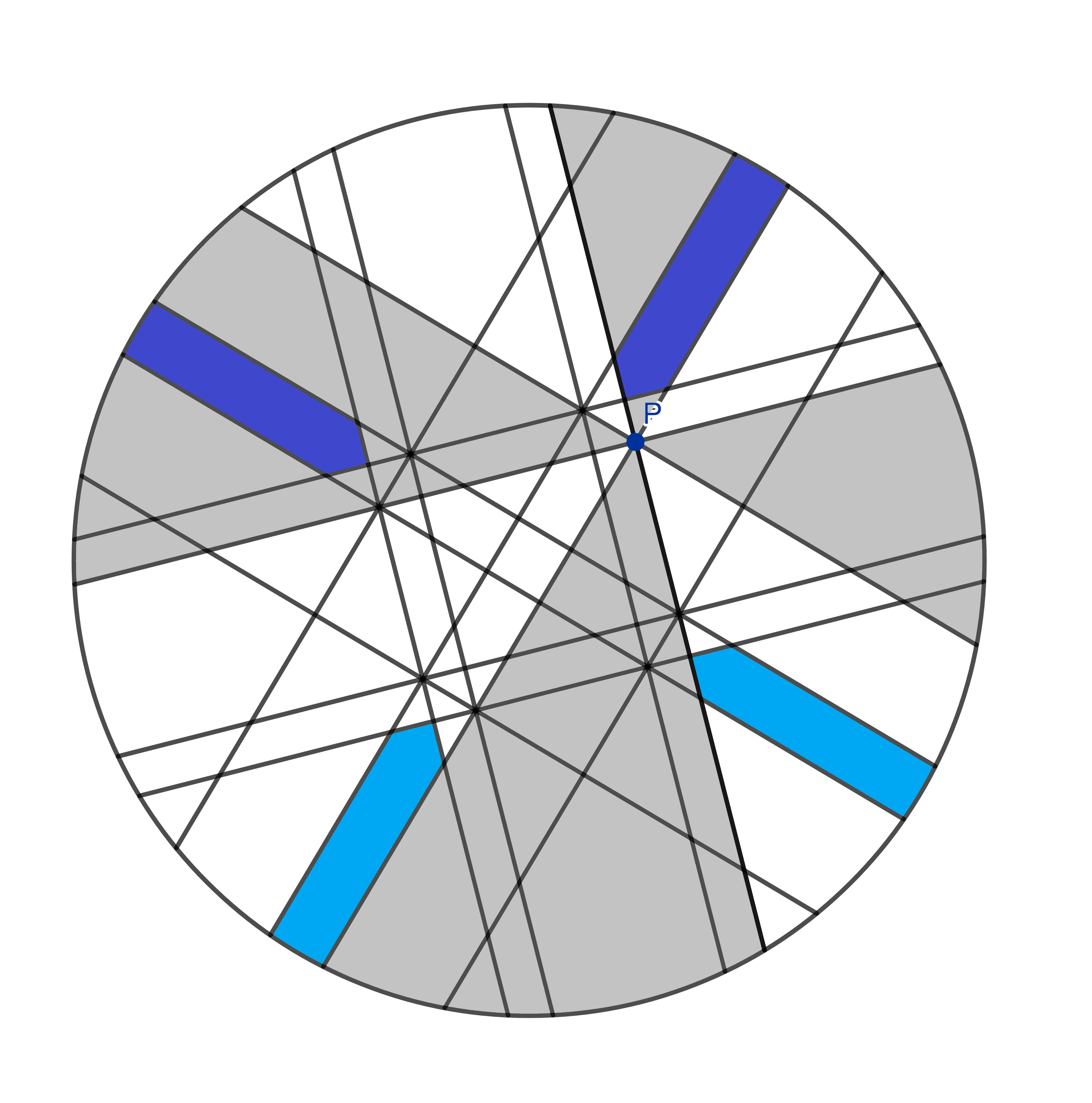
Parfait! Nous avons quatre de ces formes, qui sont toutes des images miroir parfaites les unes des autres et qui ont donc la même taille. Et regardez, deux d’entre elles font partie de vos tranches et deux font partie des miennes. Mangeons-les et nous aurons tous les deux mangé la même quantité de pizza jusqu’à présent.

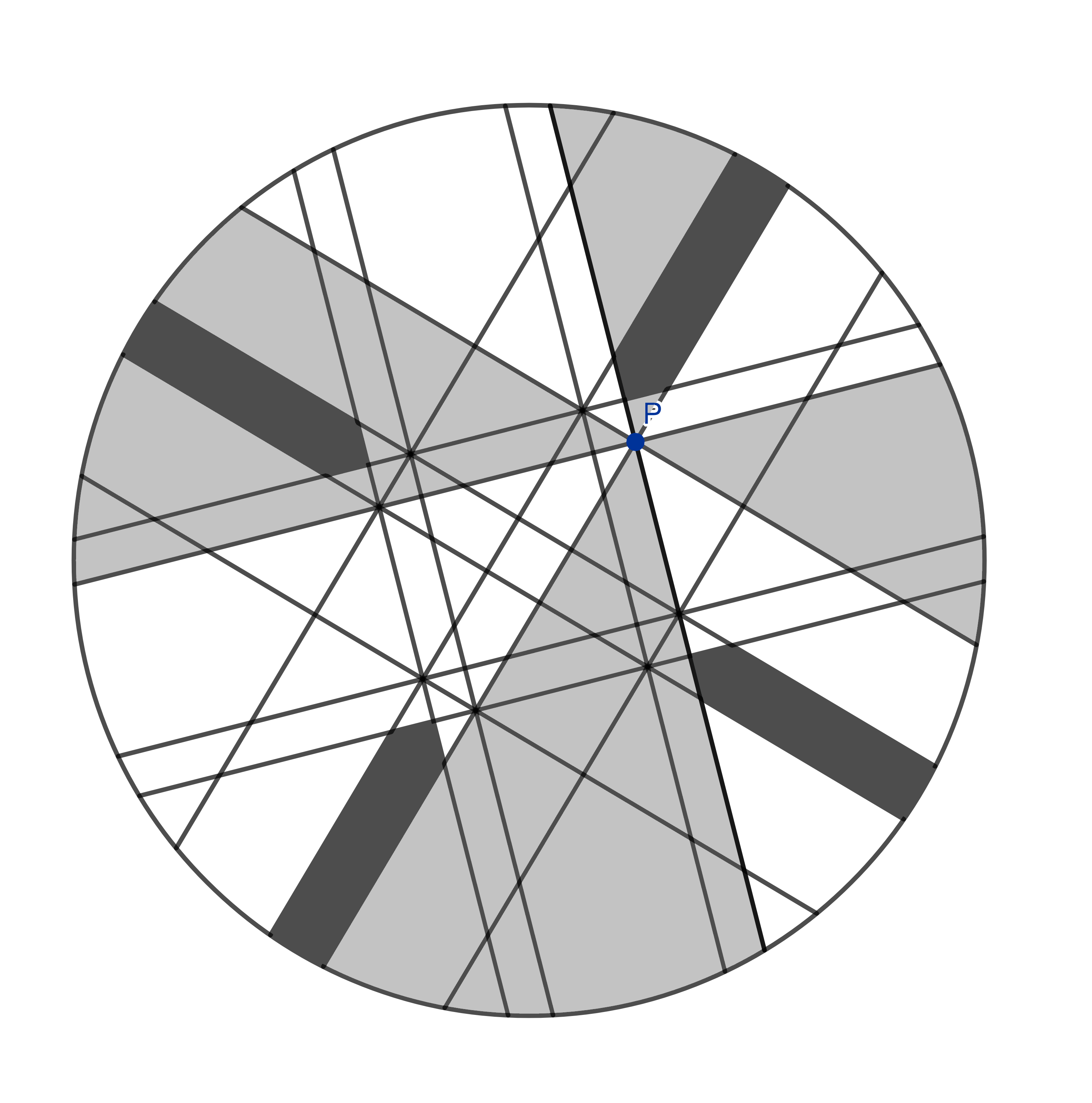
Voyons la suite.

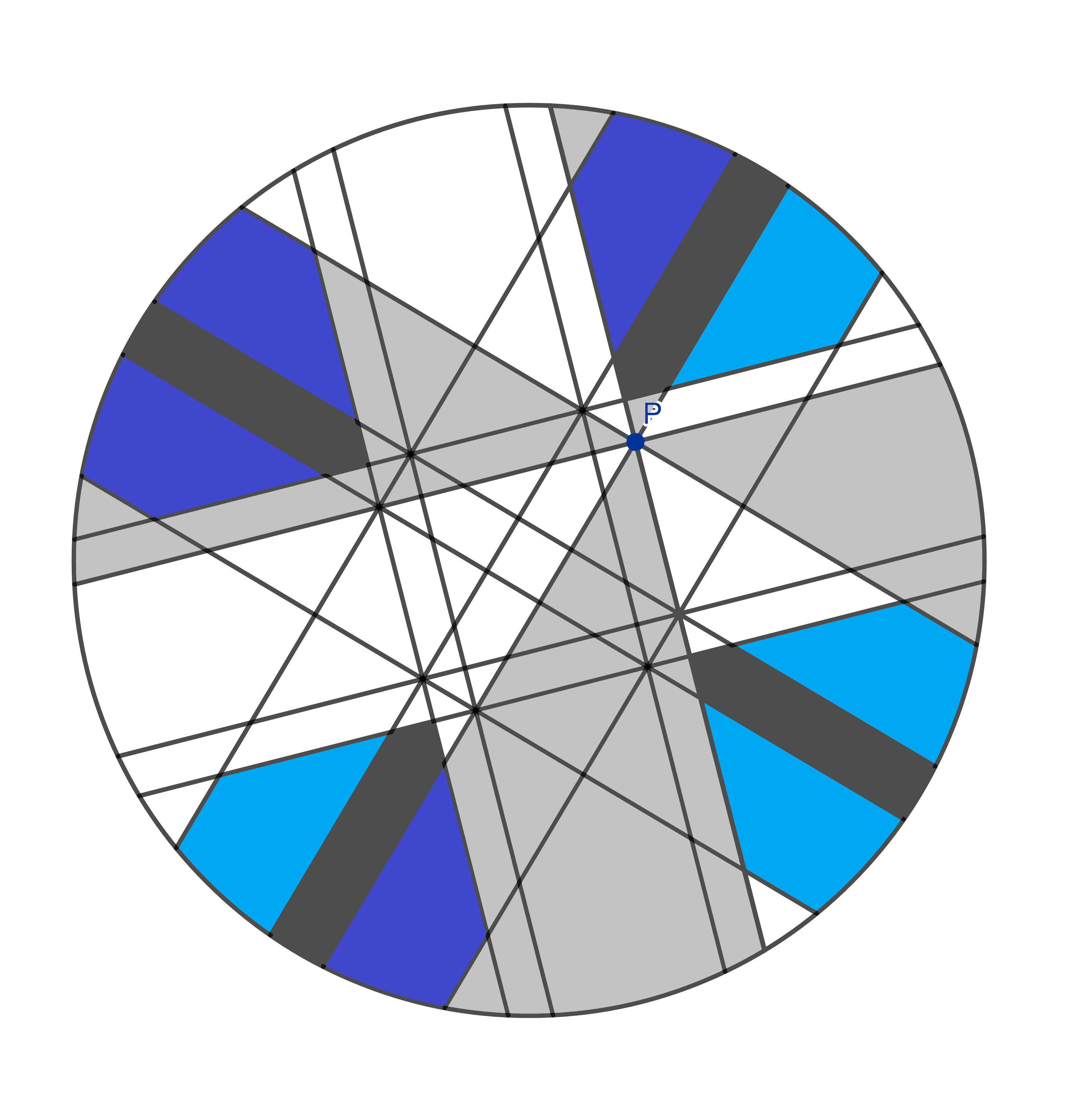
Il y a ces tranches plus épaisses, une de chaque côté des quatre formes que nous venons de manger. Nous en avons donc huit au total et, encore une fois, quatre d’entre elles sont les vôtres et quatre sont les miennes. Bon appétit!

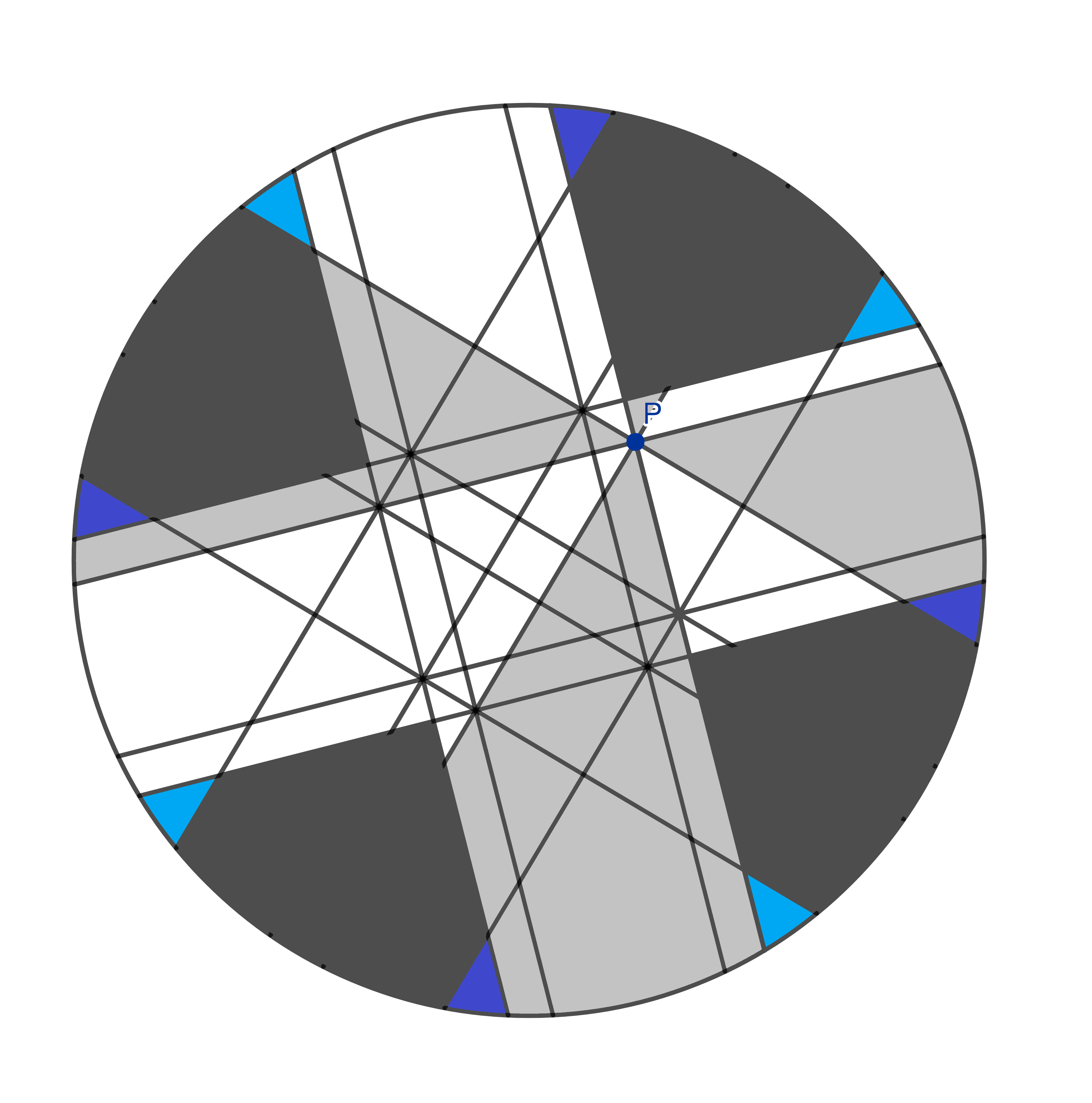
À côté des tranches plus épaisses, nous avons les morceaux qui ressemblent à des triangles. Là encore, il y en a huit, quatre m’appartiennent et quatre sont à vous. C’est l’heure du dîner!

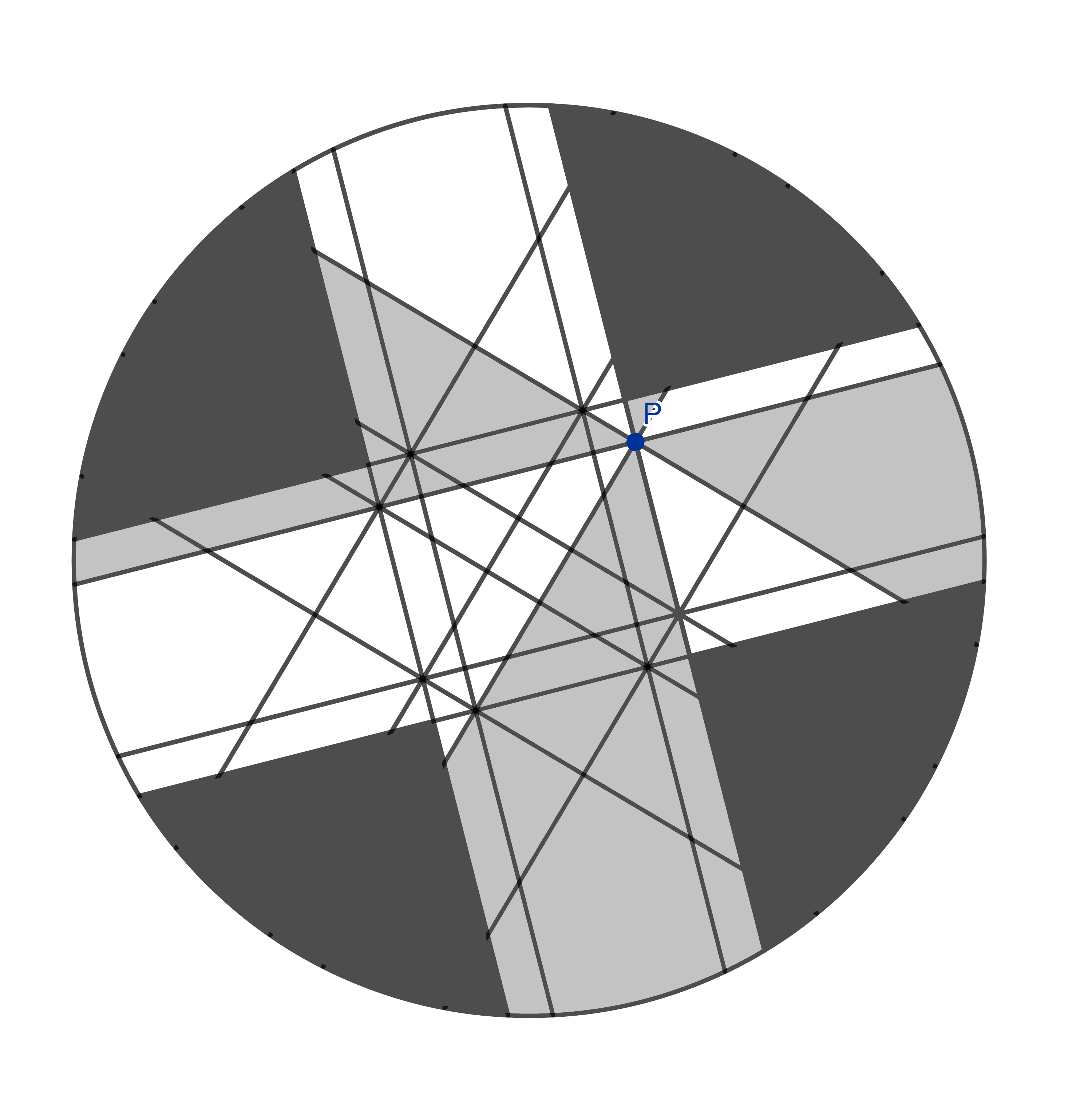
Nous continuons ainsi, en trouvant toujours des formes congruentes. Ces formes sont au nombre de huit…

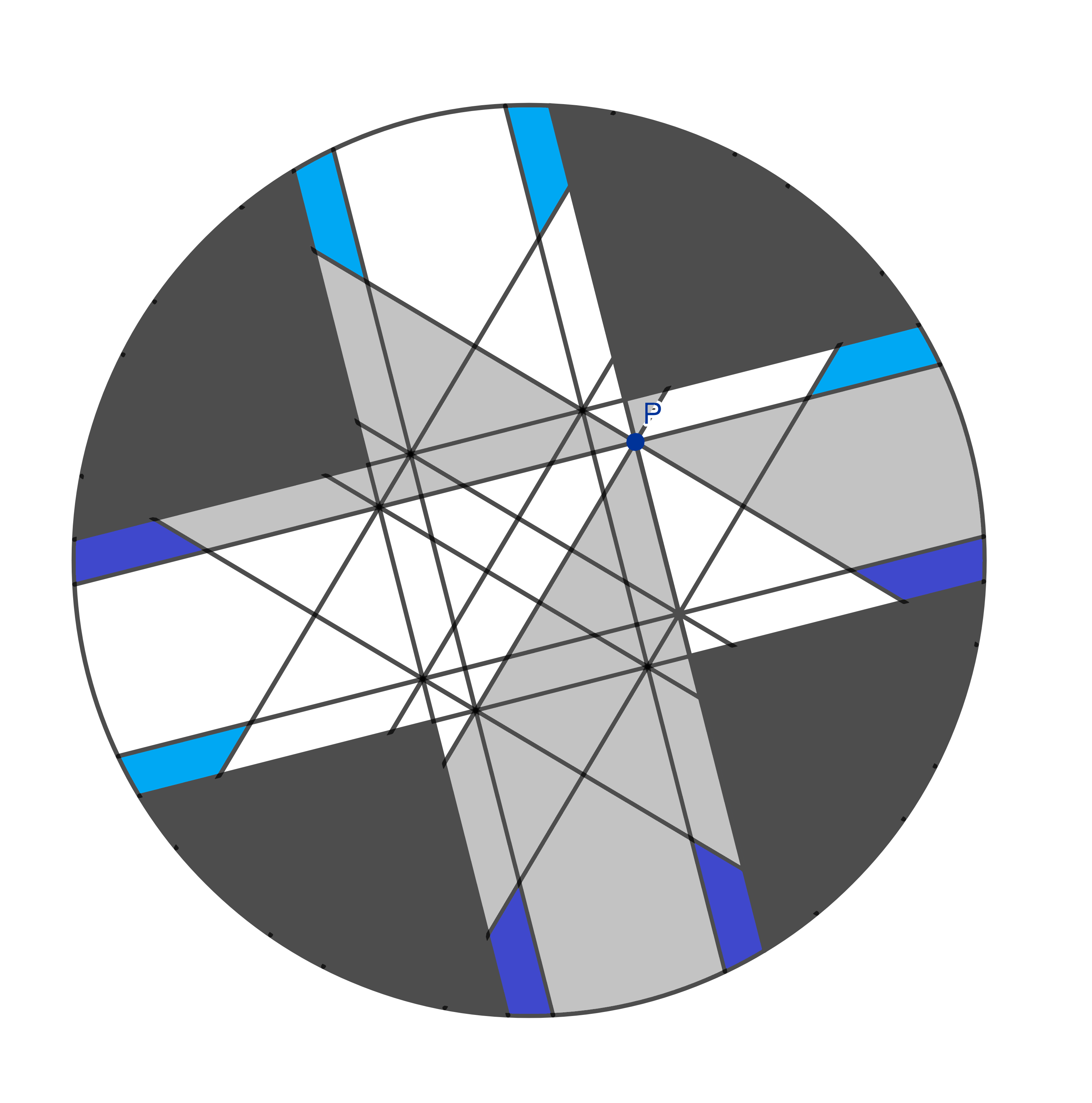
…huit d’entre eux…

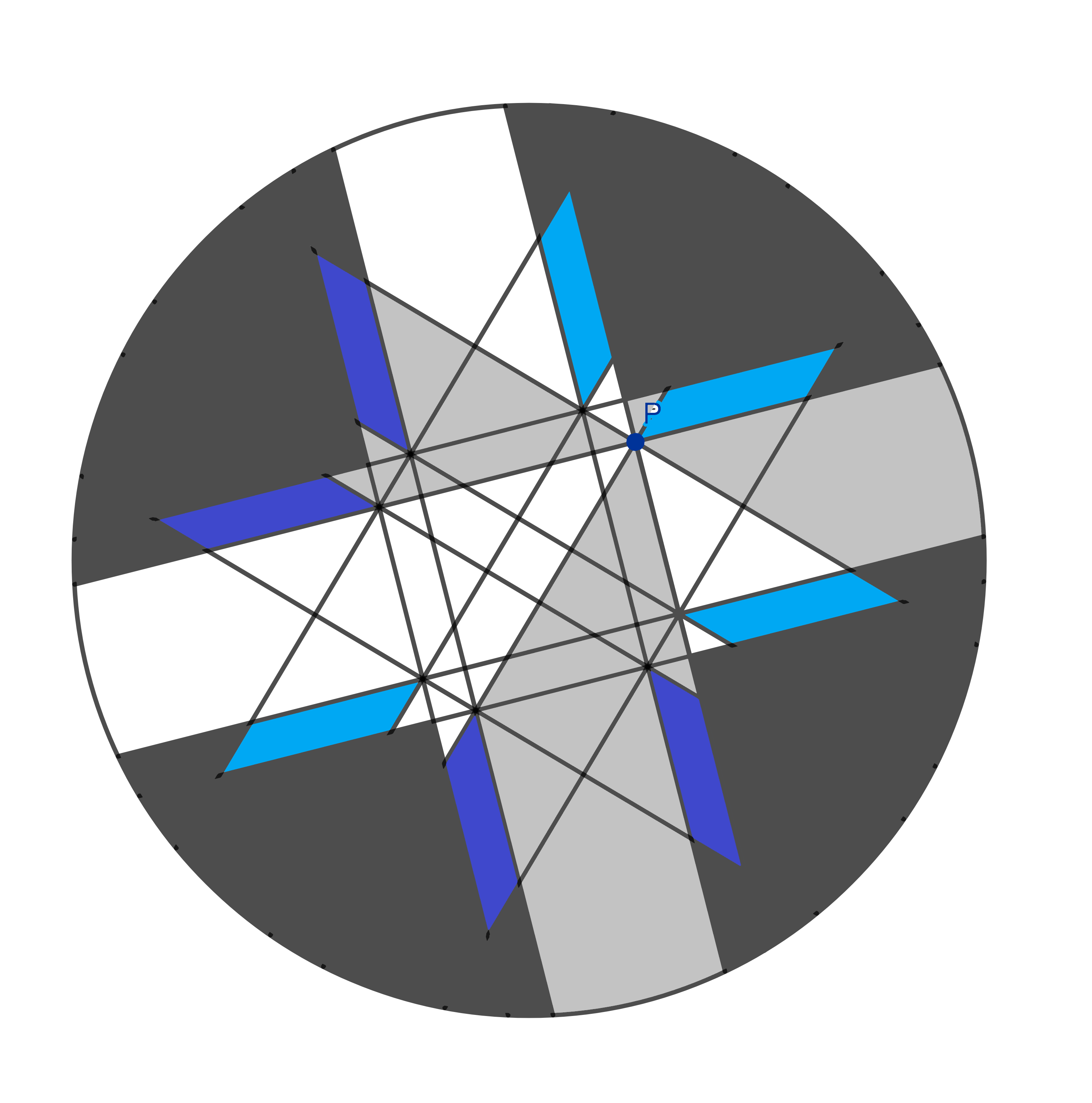
…et quatre autres de ce type.

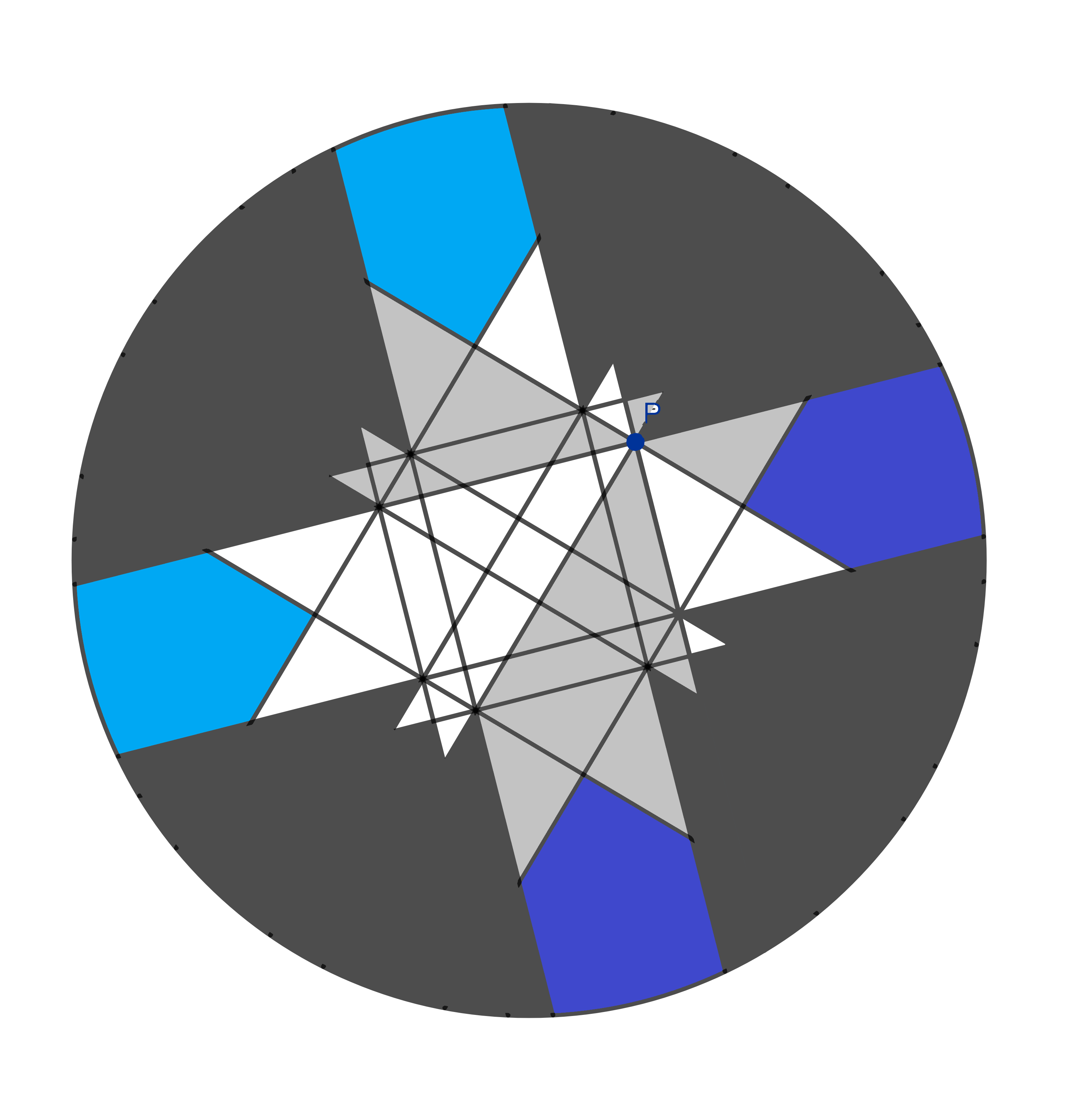
Nous avons presque terminé ! Il y a 12 des plus grands triangles, six pour nous deux…

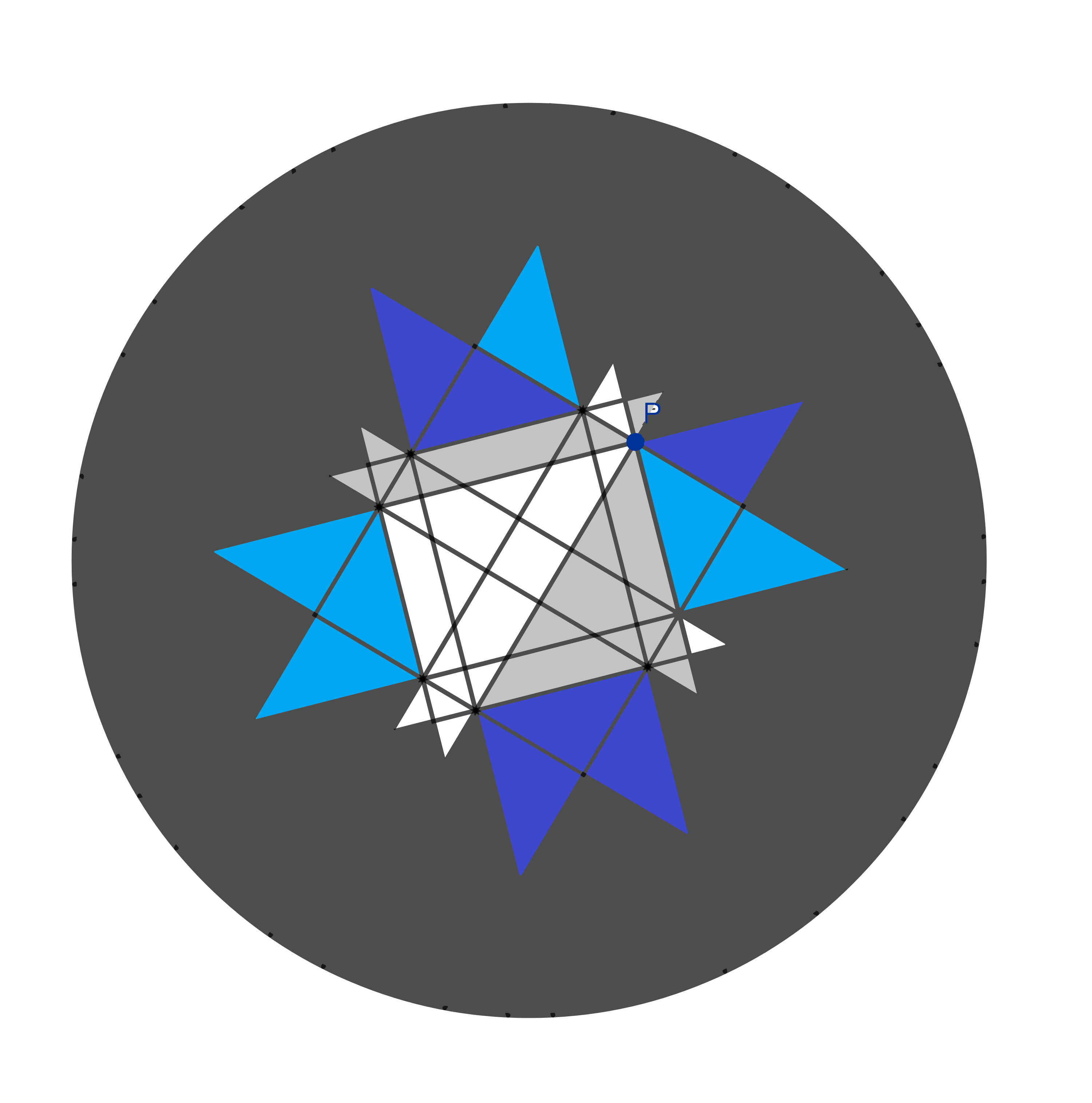
…et 12 triangles plus petits.

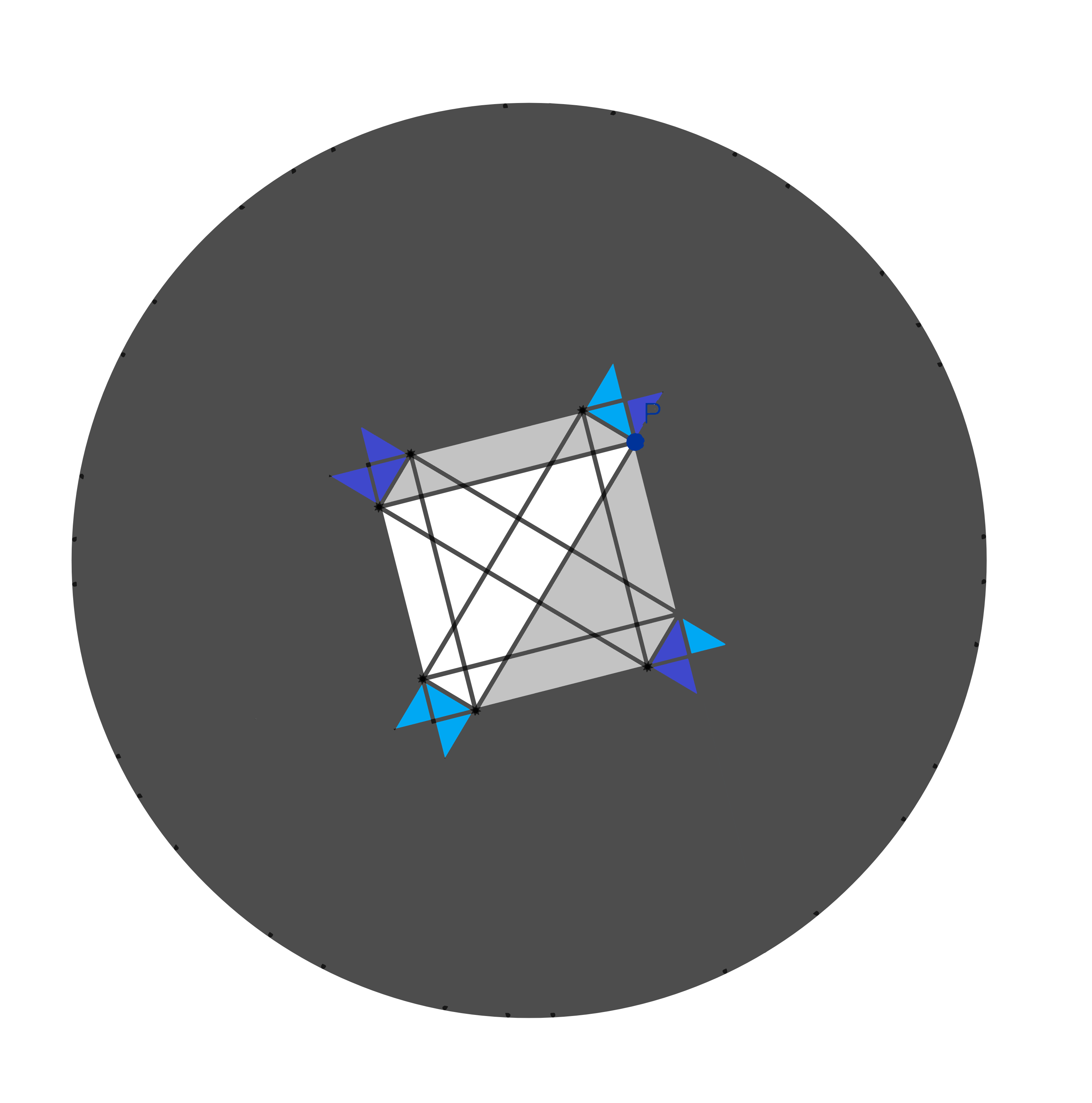
Pour la partie restante, je ferai une coupe supplémentaire en rouge.

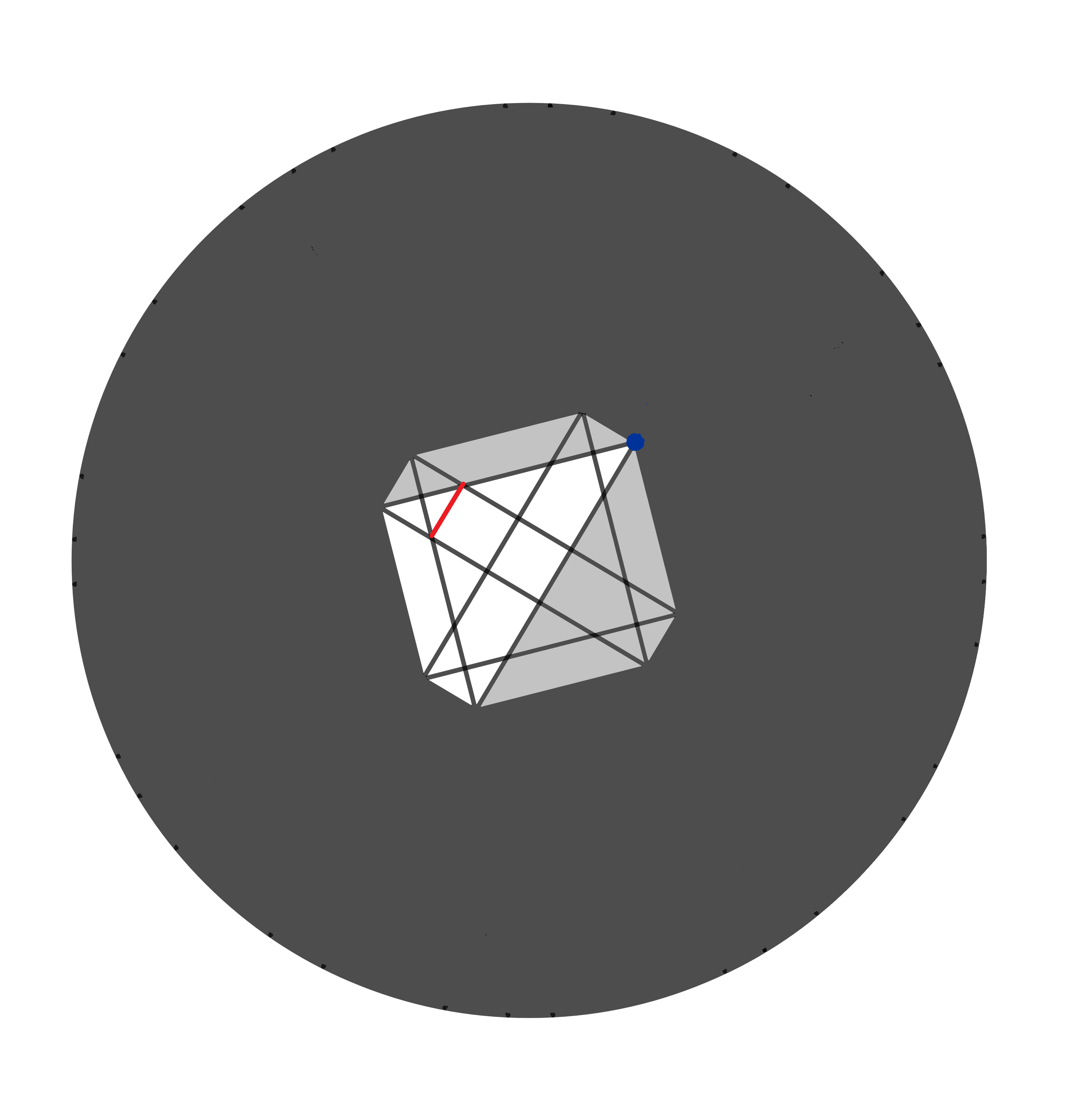
Ensuite, nous obtenons tous les deux un grand trapèze…

…trois petits triangles…

…et enfin un trapèze plus fin.

Et c’est tout. Nous avons mangé toute la pizza et à chaque étape, nous avons eu les mêmes parts!

Essayez vous-même

Saisissez et déplacez le point de coupe dans le cercle et voyez si vous pouvez trouver les tranches congruentes.